Ratio problems are often solved by using proportions. A proportion is an equation formed with two ratios that are equal. One method for solving a proportion problem is to find the appropriate equivalent ratio. We could have solved the original problem by setting up a proportion and then finding what the equivalent fraction would have to be.
Example: The ratio of girls to boys in the chess club is a 2 to 1. If there are 10 boys in the chess club, how many girls are there in the club?
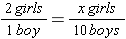
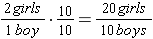
So when there are 10 boys, there must be 20 girls. Note that we wrote the ratios in the proportion in the fraction form and that the second ratio must be in the same order as the first ratio. In this case the numerals representing the number of girls are in the numerators and the numerals representing the number of boys are in the denominators.
Example: A student attends only 3 out of every 4 days during a summer course. If the student attended 15 days, how many days did the summer course run?
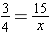
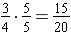
Note that this time the missing value is in the denominator, since the denominator in the first ratio is days attended to total days.
The summer school course was 20 days long.
Be Careful with the Wording: We need to watch the wording carefully when working any ratio or proportion problem.
Example: A state lottery sells scratch tickets and guarantees that one out of every six tickets is a winning ticket.
(a) Express the ratio of winning tickets to losing tickets in simplest form.
Be careful. The ratio of winning tickets to losing tickets is not 1 : 6. The correct ratio is 1 : 5, since on average out of six tickets we would expect one winning ticket and five losing tickets.
(b) How many tickets would you expect to have to buy in order for three of them to be winners?
Since we are looking for the total tickets, we use the ratio of the winning tickets to the total number of tickets, which is 1 : 6. The proportion for the problem would then be 
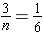, since we desire three winning tickets but do not know the expected total. We solve the problem using equivalent ratios
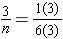
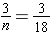
To obtain three winning tickets, we would expect to have to buy about 18 tickets. In practice, if we were to actually buy 18 tickets, we may not actually get exactly 3 winning tickets, since this is actually a probability question where the number of tickets could be more or less than 18 tickets, but the average expected number would be 18.
If a beverage company advertices one of every eight bottles of pop wins a free bottle of pop, how many winning bottles would one expect in a gross
?
A mother of three is pregnant with her fourth child.
One evening, the eldest daughter says to her dad: "Dad, do you know what I just found out?"
"No."
"The new baby will be Chinese!"
"What?!"
"Yes. I just read in the paper that statistics shows that every fourth child born nowadays is Chinese."
Content ©2010. All Rights Reserved.
Date last modified: July 6, 2010.
Created with SoftChalk LessonBuilder
By Kris Montis and Timothy Peil
