3.1.1 Introduction to Transformational Geometry  Printout
To state a theorem and then to show examples of it is literally to teach backwards.
—Kim Nebeuts, Return to Mathematical Circles (1988)

      The approach taken in the topics of Chapter 2 was static in that the objects studied were fixed in position. In this chapter, a more dynamic approach is taken in the study of neutral and Euclidean geometry. We will make a comparison between objects with the idea of moving one object onto another object that is similar. The concept of a transformation is a function that maps a set onto another set, i.e., in some sense, motion is introduced through one-to-one and onto functions, called transformations. For example, we will study principles and concepts used in creating animations in computer graphics. Physically, we move one object such as a chair next to another chair to compare them for size, shape, color, and other properties.
     The wallpaper pattern, on the left, illustrates several of the topics we will be studying. Notice that the wallpaper pattern is symmetric with respect to either of the two diagonal lines; this is an example of a line reflection. Each individual snowflake also has line symmetry. How many lines of symmetry does each individual snowflake have? The wallpaper pattern also shows rotation symmetry; rotations of 90°, 180°, and 270°. Also, the top row can be slid (translated) to match the bottom row. What other types of transformations does this wallpaper pattern exhibit? The mathematics of wallpaper patterns is related to how crystallographers classify crystals (crystallography); a wallpaper pattern is just the two-dimensional version of a crystal. The restrictions to the symmetries of crystals leads to 17 possible basic wallpaper patterns. Many websites and books discuss the mathematics of wallpaper patterns.
      A generalization of wallpaper patterns is plane tilings. The plane tiling, on the right, illustrates several transformations. What types of transformations can you identify (rotation, reflection, translation, etc.)? What is the basic unit of this plane tiling? A plane tiling is created by covering a plane completely with some basic shapes such as a regular polygon (uniform tiling). When one shape is used as the basic unit, the plane tiling is called a tesselation. Is the figure on the right a tessellation?
      M. C. Escher (1898–1972), a Dutch graphic artist, drew many illustrations using the concepts of symmetry. Here are some websites with Escher's illustrations: M.C. Esher official website,  World of Escher, and Escher Pages with links to other Escher web sites and books.

Click here to explore a dynamic illustration of a tessellation with GeoGebra html or JavaSketchpad.

      Another example of the use of transformations is in frieze patterns, as in the examples above and below. What types of transformations are used in the frieze patterns? (translation, reflection, rotation, etc.?)

      Examples of transformations from the physical or natural world. What types of transformations and symmetries are illustrated with each?

      Before we begin our study of transformational geometry, examine the following diagrams. Use the diagrams and the above illustrations to write a precise definition of each type of transformation.       

Click here to explore dynamic illustrations of transformations GeoGebra html or JavaSketchpad (translate, rotate, reflect, dilate, shear, strain) shown in the following diagrams.

Translation by Vector PQ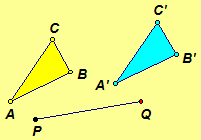	Rotation about O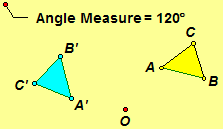
Reflection in a Line	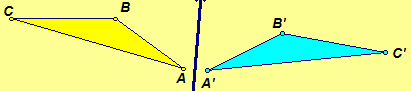Reflection through a Point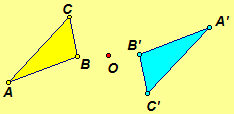
Glide Reflection by Vector PQ	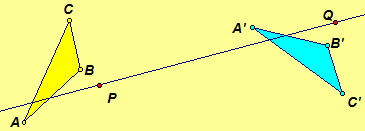Dilation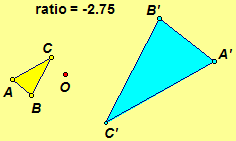
Shear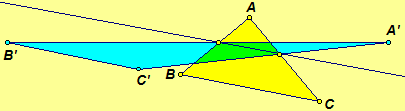	Strain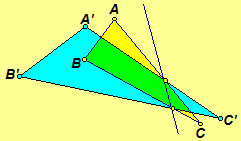

Geometer's Sketchpad or GeoGebra prepared diagrams for further investigation are located in Appendix B of the Course Title Page Prepared Geometer's Sketchpad and GeoGebra Sketches.

Investigation Exercise 3.1. (a) Construct a tessellation. (Directions for construction.) (b) What is the distance traveled by each vertex of an equilateral triangle, if it is rotated around the inside of a square with sides twice the length of the sides of the triangle? (See the prepared Geometer's Sketchpad  and GeoGebra sketches.)

A long time ago, I chanced upon this domain in one of my wanderings; I saw a high wall and as I had a premonition of an enigma, something that might be hidden behind the wall, I climbed over with some difficulty. However, on the other side I landed in a wilderness and had to cut my way through with great effort until—by circuitous route—I came to the open gate, the open gate of mathematics.
—M. C. Escher (1898–1972)