TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

    3.5.1 Reflections and Glide Reflections  Printout
The mathematical sciences particularly exhibit order, symmetry, and limitation; and these are the greatest forms of the beautiful.
—Aristotle (384–322 B.C.)

Definition.  A reflection in a line l  is a transformation of a plane, denoted R_l, such that if X is on l, then R_l(X) = X, and if X is not on l, then R_l maps X to X' such that l is the perpendicular bisector of  The line l is called the axis of the reflection.

Definition.  A glide reflection, denoted G_PQ, is the composition of the reflection with axis  and the nonidentity translation T_PQ, i.e. .

Investigation Exercises. Is each transformation an isometry? If yes, is it a direct or indirect isometry?
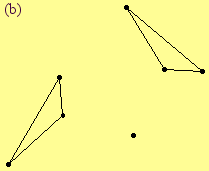
3.67.  Draw a right triangle  with right angle at C. Accurately draw its image under each transformation.
     (a)  R_l where  

     (b)  R_l where
     (c)  G_AC

     (d)  G_BC

3.68.  Draw the image of each transformation (a)  R_l  (b)  G_PQ.

            
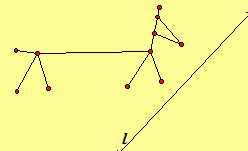
Click here to investigate dynamic illustrations of the above diagrams with GeoGebra or JavaSketchpad.

3.69. 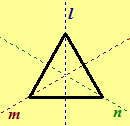 Complete the table of the compositions of symmetries for an equilateral triangle. An animation sketch is available for Geometers Sketchpad in Geometers Sketchpad and GeoGebra Prepared Sketches and Scripts.

	I = RO,0	RO,120	RO,240	Rl	Rm	Rn
I = RO,0
RO,120
RO,240
Rl
Rm
Rn

       Is the set of symmetries of an equilateral triangle a group? Explain.

3.70.  Complete a table of the compositions of the symmetries for a square. Is the set of symmetries of a square a group? Explain.

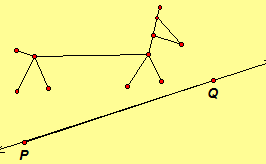
3.71.  For each diagram, draw the axes of a composition of reflections that map one triangle onto the other triangle. What is the fewest number of axes of reflection that can be drawn?

Theorem 3.19. A reflection of a neutral plane is an isometry.

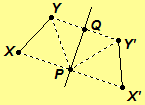      Proof.  Let R_l be a reflection of a neutral plane. Let X and Y be any two distinct points with X' = R_l(X) and Y' = R_l(Y). We need to show XY = X'Y'. One of the following is true: (1) X and Y are on the same side of l. (2) X and Y are on opposite sides of l. (3) One of X and Y are on l. (4) Both X and Y are on l. We prove case 1 and leave the other cases as an exercise.
      Assume X and Y are on the same side of l. By definition of the reflection R_l, l is the perpendicular bisector of segments  and  Hence, there are points P and Q on l such that , , , and  Thus, since , we have  by SAS. Hence,  and  By angle subtraction, . Hence, by SAS,  Therefore, by the definition of congruent triangles and congruent segments, XY = X'Y'. The proofs that XY = X'Y' for the other cases is left as an exercise. Hence the reflection R_l  is an isometry.//

Theorem 3.20. The inverse of a reflection of a neutral plane is the reflection itself.

Theorem 3.21. Every point on the axis of reflection is invariant under a reflection of a neutral plane.

Theorem 3.22. All lines perpendicular to the axis of reflection are invariant under a reflection of a neutral plane.

Theorem 3.23. For any two distinct points X and Y in a neutral plane, there exists exactly one reflection that maps X to Y.

Proof.  Let X and Y be two distinct points in a neutral plane. There exists a unique perpendicular bisector l of the segment  Hence, by the definition of a reflection, R_l is the unique reflection that maps X to Y.//

Theorem 3.24. A glide reflection of a Euclidean plane is an isometry.

Theorem 3.25. The axis of a glide reflection is the only invariant line under a glide reflection of a Euclidean plane.

Theorem 3.26. A glide reflection of a Euclidean plane has no invariant points.

Theorem 3.27. Every isometry of a Euclidean plane is the composition of at most three reflections. (For a dynamic diagram, GeoGebra or JavaSketchpad.)

Proof.  Let f be an isometry of a Euclidean plane, and let X, Y, and Z be any three noncollinear points. Further, let X' = f(X), Y' = f(Y), and Z' = f(Z).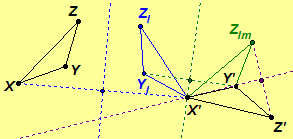 By Corollary 3.10, we only need to find a composition of three reflections that maps X, Y, and Z to X', Y', and Z', respectively. If X and X' are distinct, then by Theorem 3.23 there is a unique reflection R_l that maps X to X'. Let Y_l = R_l(Y) and Z_l = R_l(Z).  Similarly, if Y_l and Y' are distinct, there is a unique reflection R_m that maps Y_l to Y'. Since f and R_l are isometries, X'Y' = XY = X'Y_l. Hence, X' is on line m the perpendicular bisector of  and X' = R_m(X'). Thus, the composition  maps X to X', Y to Y', and Z to some point Z_lm. As before, if Z_lm and Z' are distinct, there is a unique reflection R_n that maps Z_lm to Z'. Since f, R_l, and R_m are isometries, X'Z' = XZ = X'Z_l = X' Z_lm and Y'Z' = YZ = Y_lZ_l = Y' Z_lm. Hence, X'  and Y' are on line n the perpendicular bisector of , X' = R_n(X') and Y' = R_n(Y'). Thus, the composition  maps X to X', Y to Y', and Z to Z'. If X = X', Y_l = Y', or Z_lm = Z', then omit R_l, R_m, or R_n, respectively, from the composition. By Theorem 3.20, the identity transformation is the composition of a reflection with itself. Therefore, every isometry of a Euclidean plane is the composition of no more than three reflections.//

Theorem 3.28. Every isometry of a Euclidean plane is a translation, rotation, reflection, or glide reflection.

Exercise 3.72.  Repeat Exercise 3.71 by following the method given by the proof of Theorem 3.27.

Exercise 3.73.  Complete the proof of Theorem 3.19 for the other cases.

Exercise 3.74.  Prove Theorem 3.20.

Exercise 3.75.  Prove Theorem 3.21.

Exercise 3.76.  Prove Theorem 3.22.

Exercise 3.77.  Prove Theorem 3.24.

Exercise 3.78.  Prove Theorem 3.25.

Exercise 3.79.  Prove Theorem 3.26.