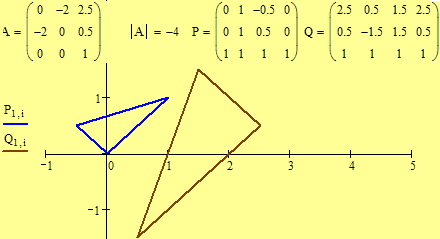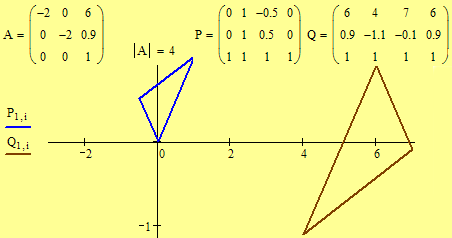TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

3.6.2 Similarity for the Analytic Euclidean Plane Model Printout
I believe the geometric proportion served the creator as an idea when He introduces the continuous generation of similar objects from similar objects.
—Johannes Kepler (1571–1630)

       The matrix of an affine similarity may be found by a method that is analogous to the method used in determining the matrix of an affine isometry.

Proposition 3.16. An affine transformation of the Euclidean plane is a similarity with ratio r if and only if the matrix representation is

 (direct similarity)
 or       (indirect similarity).

Corollary to Proposition 3.16. The determinant of a direct similarity is r² and the determinant of an indirect isometry is –r².

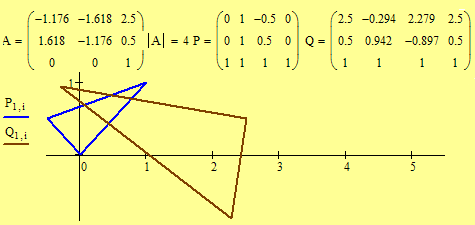
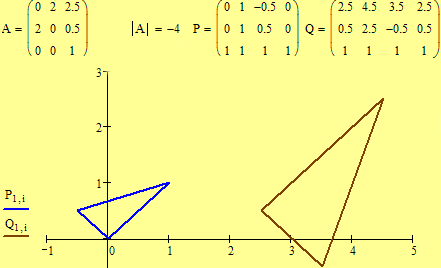
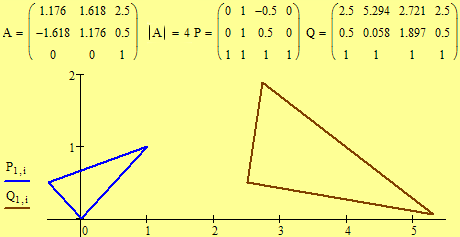
Examples. Which is a direct similarity? Which is an indirect similarity? Note the positions of the triangles.

Matrix A is the similarity matrix.
Matrix P is the matrix of the three endpoints of the original triangle.
Matrix Q = AP is the matrix of the transformed endpoints.
Click here to view an animation of the following two examples.

Click here to view an animation of the following two examples.

      The matrix for an affine dilation may be found by following the procedures as with the other matrix derivations.

Proposition 3.17. An affine transformation of the Euclidean plane is a dilation with ratio r and center C(c₁,c₂) if and only if the matrix representation is

 

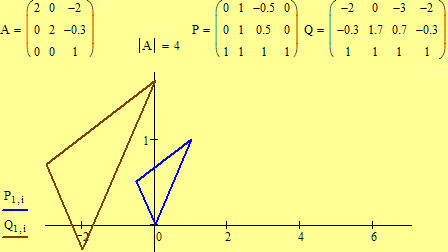
Examples.  Are the following dilations direct or indirect similarities?

Click here to view an animation of the following two examples.

Exercise 3.103. Let C(–2, –3, 1), X(1, 3, 1), and X'(2, 5, 1). (a) Show the three points are collinear. (b) Find the matrix of a dilation with center C that maps X to X'.  (c)  Find the image of (–4, 7, 1) under this dilation.  (d) Find the image of the line l[1, 1, 1] and m[1, 1, –1] under this dilation.

Exercise 3.104. Find a matrix of a similarity that maps X(1, 2, 1) to X'(2, 4, 1) and Y(0, 0, 1) to Y'(–4, 2, 1), then find the image of Z(3, 10, 1).

Exercise 3.105. Find a matrix of a similarity that maps X(0, 0, 1) to X'(5, 0, 1) and Y(1, 0, 1) to Y'(5, 8, 1), and Z(1, 1, 1) to Z'(–3, 0, 1), then find the image of P(4, –3, 1).

Exercise 3.106. Show a derivation for Proposition 3.16.

Exercise 3.107. Show a derivation for Proposition 3.17.