Exercises for Chapter Three Printout
You know you've got to exercise your brain just like your muscles.
—Will Rogers (1879–1935)

Investigation Exercise 3.1. (a) Construct a tessellation. (Directions for construction.) (b) What is the distance traveled by each vertex of an equilateral triangle, if it is rotated around the inside of a square with sides twice the length of the sides of the triangle? (See the prepared Geometer's Sketchpad sketches.)

Exercise 3.2. Which of the following mappings are transformations? Justify.

a. such that .

b. such that .

c. such that .

d. such that .

e. Let P be a point in a plane S. Define by f(P) = P and for any point , f(Q) is the midpoint of .

Exercise 3.3. Let and be transformations defined respectively by f(x ,y) = (x – 4, y + 1) and g(x, y) = (x + 2, y + 3).

a. Find the composition .

b. Find the composition .

c. Find the inverse of f, f ^–1.

d. Find the inverse of g, g ^–1.

Exercise 3.4. Prove the composition of two transformations of a plane is a transformation of the plane.

Exercise 3.5. (a) Prove the identity function is a transformation. (b) Prove the inverse of a transformation of a plane is a transformation of the plane. (c) Prove the composition of functions is associative.

Exercise 3.6. Find two lines l[l₁ ,l₂, l₃] through the point (2, –3, 1).

Exercise 3.7. Given the line [4, –2, 3]. (a) Write two other sets of homogeneous coordinates for the line. (b) Write an equation of the line. (c) Find two distinct points (x₁, x₂, 1) on the line.

Exercise 3.8. Find the line l[l₁, l₂, l₃] for each problem. (a) x₁-axis. (b) x₂-axis. (c) The line where all points have the same first and second coordinates.

Exercise 3.9. (a) What are the coordinates of the origin? (b) Find the general form of a line l[l₁, l₂, l₃] through the origin.

Exercise 3.10. Find the two lines l[l₁ ,l₂, l₃] that represent the two coordinate axes.

Exercise 3.11. Find the line l[l₁, l₂, l₃] that contains the points (3, 5, 1) and (–7, 3, 1).

Exercise 3.12. Find the point of intersection of the lines [–2, 4, –3] and [3, –5, 2].

Exercise 3.13. Use the propositions to justify your answer for the following. (a) Are the points (8, 2, 1), (7, 5, 1), and (5, 11, 1) collinear? (b) Are the lines [4, 2, 3], [–3, 1, 0], and [2, –7, 3] concurrent?

Exercise 3.14. Use the definition to find the measure of the angle between each pair of lines. (a) [–2, 4, –3] and [3, –5, 2]. (b) The coordinate axes.

Exercise 3.15. (a) What is the relationship between the coordinates of two distinct parallel lines? Justify the expressions. (b) Based on the definition of the measure of an angle between two lines, what is the measure of the angle between two parallel lines?

Exercise 3.16. Prove the relation used in defining lines is an equivalence relation.

Exercise 3.17. The steps in the converse of the proof of Proposition 3.1 are reversible, but require that the nontrivial solution, [a₁, a₂, a₃], of the matrix equation cannot have both a₁ and a₂be zero. Prove that this is true, which completes the proof of the theorem.

Exercise 3.18. Prove Proposition 3.2.

Exercise 3.19. Prove that every affine transformation of the Euclidean plane has an inverse that is an affine transformation of the Euclidean plane. (Hint. Write the inverse by using the adjoint. Refer to a linear algebra text.)

Exercise 3.20. Prove Proposition 3.3.

Exercise 3.21. Given three points P(0, 0, 1), Q(1, 0, 1), and R(2, 1, 1), and an affine transformation T. (a) Find the points P' = T(P), Q' = T(Q), and R' = T(R) where the matrix of the transformation is . (b) Sketch triangle PQR and triangle P'Q'R' . (c) Describe how the transformation moved and changed the triangle PQR.

Exercise 3.22. Find the matrix of an affine transformation that maps P(0, 0, 1) to P'(0, 2, 1), Q(1, 0, 1) to Q'(2, 1, 1), and R(2, 3, 1) to R'(7, 9, 1).

Exercise 3.23. Show the group of affine transformations of the Euclidean plane is not commutative.

Exercise 3.24. Which of the following transformations are isometries? Justify.

a. such that .

b. such that .

c. such that .

d. such that .

e. such that .

f. Let P be a point in a plane S. Define by f(P) = P and f(Q) to be the midpoint of for any point .

Exercise 3.25. Show that collinearity in a Euclidean plane is not necessarily invariant under a transformation. (Hint. Consider such that .)

Exercise 3.26. Prove congruence (as defined in Section 3.3) is an equivalence relation.

Exercise 3.27. Prove. If then AB = CD.

Exercise 3.28. Prove. Assume f is an isometry. If then

Exercise 3.29. Prove Corollary 3.2.

Exercise 3.30. Prove Corollary 3.4.

Exercise 3.31. Prove Corollary 3.5.

Exercise 3.32. Prove Corollary 3.7.

Exercise 3.33. Fill in the details for the first case in the proof of Theorem 3.9, that the ruler postulates, Theorem 3.1, and Corollary 3.4 do imply f(P) = P.

Exercise 3.34. Prove Corollary 3.10. (Show both existence and uniqueness of the isometry.)

Exercise 3.35. Find an affine transformation of the Euclidean plane that is not an isometry.

Exercise 3.36. (a) Verify the above example. (b) Find the matrix of an affine transformation that maps p[1, 2, 3], q[–1, 3, 1], and r[2, –1, 5] to p'[1, 0, 2], q'[–1, 5, –8], and r'[2, –5, 13], respectively. (Hint. Need to solve a system of nine equations and nine variables. You may use a calculator or computer to solve the system.)

Exercise 3.37. Let A(0, 0, 1), B(1, 0, 1), C(0, 1, 1), D(1, 1, 1), E(2, 1, 1), and F(1, 2, 1). Show the sets {A, B, C} and {D, E, F} are congruent. (Two sets of points are said to be congruent provided there is an isometry where one set is the image of the other set.)

Exercise 3.38. An affine transformation maps X(5, 0, 1) to X'(4, 6, 1) and Y(0, 0, 1) to Y'(1, 2, 1). (a) Show d(X, Y) = d(X', Y') and show the transformation may not be an isometry. (b) Find a direct isometry for the transformation. (c) Find an indirect isometry for the transformation. (d) Find the image of Z(3, 10, 1) for the isometries you obtained in parts (b) and (c).

Exercise 3.39. Complete the proof of Proposition 3.7.

Exercise 3.40. Prove Proposition 3.8.

Exercise 3.41. Prove Proposition 3.9.

Exercise 3.42. Prove Proposition 3.10.

Exercise 3.43. Fill in the missing steps of the two computations in the proof of Proposition 3.11.

Exercise 3.44. Prove the inverse of an indirect isometry is an indirect isometry.

Exercise 3.45. Prove Proposition 3.12. (Note Exercise 3.44.)

Investigation Exercises. Is each transformation an isometry? If yes, is it a direct or indirect isometry.

3.46. Draw a right triangle with right angle at C. Accurately draw its image under each transformation.
(a) T_AC

(b) T_AM where M is the midpoint of .
(c) R_A,₉₀

(d) R_C,₁₅₀

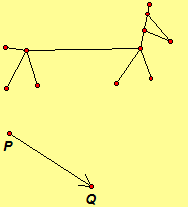
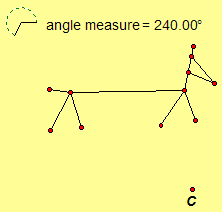
3.47. Draw the image of each transformation (a) T_PQ (b) R_c,₂₄₀ .

Diagram for Exercise 3.47(a). Diagram for Exercise 3.47(b).

3.48. Complete the table of the compositions of rotation symmetries for an equilateral triangle.

	I = R_O,₀	R_O,₁₂₀	R_O,₂₄₀
I = R_O,₀
R_O,₁₂₀
R_O,₂₄₀

Is the set of rotation symmetries of an equilateral triangle a group? Explain.

3.49. Complete a table of the compositions of the rotation symmetries for a square. Is the set of rotation symmetries of a square a group? Explain.

Exercise 3.50. Verify other subcases in Case 2 of the proof of Theorem 3.11.

Exercise 3.51. Prove Theorem 3.12.

Exercise 3.52. Prove Theorem 3.13.

Exercise 3.53. Prove Theorem 3.14.

Exercise 3.54. (a) Verify the case where C is between X and Y in the proof of Theorem 3.16. (b) Verify the angle congruence for each case when the points were assumed to be noncollinear in the proof of Theorem 3.16.

Exercise 3.55. Prove Theorem 3.17.

Exercise 3.56. Prove Theorem 3.18.

Exercise 3.57. Find a matrix of the translation that maps the point X(3, 8, 1) to Y(5, 1, 1) and find the image of Z(12, 7, 1). Is the matrix unique?

Exercise 3.58. Find a matrix of the translation that maps the line l[2, 3, –1] to m[2, 3, 5]. Is the matrix unique?

Exercise 3.59. Find a matrix of the rotation where C(2, 1, 1) and find the image of X(3, 6, 1).

Exercise 3.60. Find a direct isometry that maps X(1, 1, 1) to X'(–1, 1, 1) and Y(3, 0, 1) to Y'(0, 3, 1). Is it a translation or a rotation?

Exercise 3.61. Let the point of intersection of the lines l[1, –1, 0] and m[1, 1, –2] be the center of a rotation that maps l to m. Find the matrix of a rotation that maps l to m.

Exercise 3.62. Let the point of intersection of the lines l[–1, 5, 1] and m[3, –2, 4] be the center of a rotation that maps l to m. Find the matrix of a rotation that maps l to m.

Exercise 3.63. What is the form of the inverse of an affine translation of the Euclidean plane? Affine rotation?

Exercise 3.64. Prove the set of affine translations of the Euclidean plane is a group under matrix multiplication.

Exercise 3.65. (a) Verify part (b) of Proposition 3.13. (b) Verify part (b) of Proposition 3.14. (c) Verify part (d) of Proposition 3.14.

Exercise 3.66. Prove the set of affine rotations of the Euclidean plane with center C is a group under matrix multiplication.

Investigation Exercises. Is each transformation an isometry? If yes, is it a direct or indirect isometry.

3.67. Draw a right triangle with right angle at C. Accurately draw its image under each transformation.
(a) R_l where

(b) R_l where
(c) G_AC

(d) G_BC

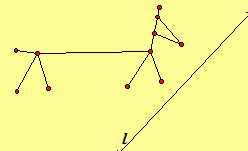
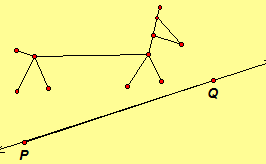
3.68. Draw the image of each transformation (a) R_l (b) G_PQ.

Draw the reflection. Draw the glide reflection.

3.69. Complete the table of the compositions of symmetries for an equilateral triangle.

Diagram showing the line symmetries of an equilateral triangle.

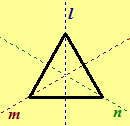
	I = R_O,₀	R_O,₁₂₀	R_O,₂₄₀	R_l	R_m	R_n
I = R_O,₀
R_O,₁₂₀
R_O,₂₄₀
R_l
R_m
R_n

Is the set of symmetries of an equilateral triangle a group? Explain.

3.70. Complete a table of the compositions of the symmetries for a square. Is the set of symmetries of a square a group? Explain.

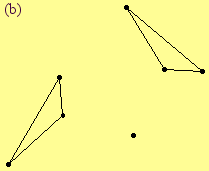
3.71. For each diagram, draw the axes of a composition of reflections that map one triangle onto the other triangle. What is the fewest number of axes of reflection that can be drawn?

Exercise 3.72. Repeat Exercise 3.71 by following the method given by the proof of Theorem 3.27.

Exercise 3.73. Complete the proof of Theorem 3.19 for the other cases.

Exercise 3.74. Prove Theorem 3.20.

Exercise 3.75. Prove Theorem 3.21.

Exercise 3.76. Prove Theorem 3.22.

Exercise 3.77. Prove Theorem 3.24.

Exercise 3.78. Prove Theorem 3.25.

Exercise 3.79. Prove Theorem 3.26.

Exercise 3.80. Find a matrix of the reflection R_l where (a) l[1, –1, 0] (b) l[0, 1, –4], then for each reflection find the image of (4, 4, 1) and

Exercise 3.81. Find a matrix of the reflection R_l where , and find the image of (2, 8, 1), (4, 4, 1), and (10, 7, 1).

Exercise 3.82. Find a matrix of the reflection that maps the point X(3, 8, 1) to Y(5, 1, 1) and find the image of Z(12, 7, 1).

Exercise 3.83. Find a matrix of the reflection that maps the line l[2, 3, –1] to m[2, 3, 5].

Exercise 3.84. Find a product of reflections that maps X(–2, 5, 1), Y(–2, 7, 1), and Z(–5, 5, 1) to X'(4, 3, 1), Y'(6, 3, 1), and Z'(4, 0, 1).

Exercise 3.85. Verify part (d) of Proposition 3.15.

Exercise 3.86. (a) Determine the inverse of a similarity with ratio r. (b) Determine the ratio of the composition of a similarity with ratio r₁ and a similarity with ratio r₂.

Exercise 3.87. Find the ratio of similarity if a 4 centimeter segment has a 6 centimeter image.

Exercise 3.88. Find the length of the image of an 8 centimeter segment under a similarity with a ratio of 3/4.

Exercise 3.89. Draw a right triangle with right angle at C. Accurately draw the triangle's image under each dilation H_O,₂, H_O,₂, and H_O,_1/2.

(a) O = C

(b) O = A

Exercise 3.90. Draw the image of each dilation H_O,₂, H_O,₂, and H_O,_1/2.

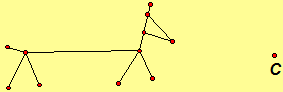
Draw the dilations.

Investigation Exercise 3.91. Each of the following larger stick figures is a similarity of the smaller stick figure where one of the figures is a dilation. Draw several more of the larger stick figures on this sheet. Can you find an similarity that maps the original dilated figure to the others?

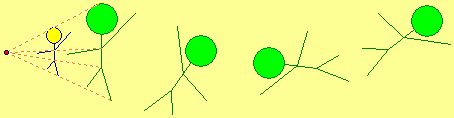
Exercise 3.92. How do the areas of a region and its image compare when the ratio of dilation is 2/3?

Exercise 3.93. Find the image of the point (3,4) under a dilation with center at the origin and ratio of –5/3.

Exercise 3.94. Prove Theorem 3.29.

Exercise 3.95. Prove Corollary 3.31.

Exercise 3.96. Prove Corollary 3.32.

Exercise 3.97. Prove Corollary 3.33.

Exercise 3.98. Prove Corollary 3.34.

Exercise 3.99. Prove Corollary 3.35.

Exercise 3.100. Prove Theorem 3.36.

Exercise 3.101. Prove the cases where r < 0 for Theorem 3.37.

Exercise 3.102. Prove Corollary 3.38.

Exercise 3.103. Let C(–2, –3, 1), X(1, 3, 1), and X'(2, 5, 1). (a) Show the three points are collinear. (b) Find the matrix of a dilation with center C that maps X to X'. (c) Find the image of (–4, 7, 1) under this dilation. (d) Find the image of the line l[1, 1, 1] and m[1, 1, –1] under this dilation.

Exercise 3.104. Find a matrix of a similarity that maps X(1, 2, 1) to X'(2, 4, 1) and Y(0, 0, 1) to Y'(–4, 2, 1), then find the image of Z(3, 10, 1).

Exercise 3.105. Find a matrix of a similarity that maps X(0, 0, 1) to X'(5, 0, 1) and Y(1, 0, 1) to Y'(5, 8, 1), and Z(1, 1, 1) to Z'(–3, 0, 1), then find the image of P(4, –3, 1).

Exercise 3.106. Show the derivation for Proposition 3.16.

Exercise 3.107. Show the derivation for Proposition 3.17.

Investigation Exercise 3.108. Suppose where a is neither 0 nor 1. Given a square PQRS with vertices P(1, 1, 1), Q(–1, 1, 1), R(–1, –1, 1), and S(1, –1, 1).

Find the image of the square for different values of a such as –3, –1, 1, 3, etc.
Describe how the transformation changed the square PQRS.
Are there any invariant points or lines? If yes, what are they?
Let
Find the image of the square PQRS with vertices P(3, 4, 1), Q(1, 4, 1), R(1, 2, 1), and S(3, 2, 1), then repeat parts (b) and (c).
Let
Find the image of the square PQRS with vertices P(1, 1, 1), Q(–1, 1, 1), R(–1, –1, 1), and S(1, –1, 1) for different values of a not 0 or 1, then repeat parts (b) and (c).
These are examples of what is called a shear. Write a general definition of a shear.
From your definition derive one or more matrices for a shear. Write any relationships you find between shears and isometries.
Write any properties you find for shears.

Investigation Exercise 1.109. Suppose where a is not –1, 0, or 1. Given a square PQRS with vertices P(1, 0, 1), Q(0, 1, 1), R(–1, 0, 1), and S(0, –1, 1).

Find the image of the square for different values of a such as –3, –1/2, 1/2, 3, etc.
Describe how the transformation changed the square PQRS.
Are there any invariant points or lines? If yes, what are they?
Let
Find the image of the square PQRS with vertices P(3, 3, 1), Q(2, 4, 1), R(1, 3, 1), and S(2, 2, 1), then repeat parts (b) and (c).
Let
Find the image of the square PQRS with vertices P(1, 0, 1), Q(0, 1, 1), R(–1, 0, 1), and S(0, –1, 1) for different values of a not –1, 0, or 1, then repeat parts (b) and (c).
These are examples of what is called a strain. Write a general definition of a strain.
From your definition derive one or more matrices for a strain.
Write any relationships you find between strains and isometries.
Write any properties you find for strains.

Investigation Exercise 3.110. Let with and

Verify the computation.
Write a theorem that the computation implies.