TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

          3.3.1 Isometry  Printout
Measure what is measurable and make measurable what is not so.
—Galileo Galilei (1564–1642)

      An important topic in the study of geometry is the concept of congruency. One way of considering figures to be congruent is when one figure is moved onto another, the figures match in every way. The size and shape of the figures are identical. This view of moving one object onto another, or physical motion, is the mathematics concept of a transformation. This section builds the tools for generalizing the concept of congruency by using transformation to fit this idea of moving an object onto another object where the property of the object moved does not vary. We begin by defining these conceptual ideas of same size (equal measure) and properties not changing (no variance). 

Definition. A transformation which preserves distance between points is an isometry.

      The prefix iso means same, equal, or identical and metry means distance. Therefore, the term isometry means equal distance, which is how we have defined the term.

Definition. A property which is preserved under a transformation is said to be invariant under the transformation.

Terminology.  A transformation of a plane in a neutral geometry will be called a transformation of a neutral plane. A transformation of a plane in a Euclidean geometry will be called a transformation of a Euclidean plane. (Remember that a neutral geometry includes both Euclidean and hyperbolic geometries. See Chapter 2.)

Theorem 3.1. Betweenness of points is invariant under an isometry of a neutral plane.

Proof.  Let f  be an isometry of a neutral plane. Let A, B, and C be three distinct points such that B is between A and C. Further, let A' = f(A), B' = f(B), and C' = f(C). By the definition of betweenness of points, AC = AB + BC and {A, B, C} is collinear. Since f is an isometry, A'C' = AC, A'B' = AB, and B'C' = BC. Hence, A'C' = AC = AB + BC = A'B' +B'C'. Thus, by the Triangle Inequality, {A', B', C'} is collinear. Therefore, B' is between A' and C'.//

Corollary 3.2. Collinearity is invariant under an isometry of a neutral plane.

Corollary 3.3. The image of a line segment (ray, angle, or triangle) under an isometry of a neutral plane is a line segment (ray, angle, or triangle).

Proof. We prove the corollary for a line segment and a ray; an angle and a triangle are left as exercises.
      Let f  be an isometry of a neutral plane. Denote f(P) = P' for every point P. By definition, segment  = {P : P = A, P = B, or P is between A and B} and ray  {P : B is between A and P}. Note that the definitions of segment and ray are dependent on betweenness of points. Hence, the result immediately follows from the invariance of betweenness of points under an isometry.//

Corollary 3.4. The image of a line segment under an isometry of a neutral plane is a congruent line segment.

Corollary 3.5. The image of a triangle under an isometry of a neutral plane is a congruent triangle.

Corollary 3.6. Angle measure is invariant under an isometry of a neutral plane.

Proof.  Given  Let f  be an isometry of a neutral plane. Denote f(P) = P' for every point P. By Corollary 3.5,  Hence  Therefore, angle measure is invariant under an isometry.//

Corollary 3.7. The image of a circle under an isometry of a neutral plane is a congruent circle.

       The above results for a neutral plane imply a more general definition for congruence for any two sets of points, which would include all figures under one definition and for any plane.

Definition.  Two sets of points are said to be congruent provided there is an isometry where one set is the image of the other set. Write  if and only if there is an isometry f such that .

Theorem 3.8. The set of isometries of a plane is a group under composition.

Proof.  Since the set of transformations of a plane is a group, we have associativity. Note that the identity transformation is an isometry since for any two distinct points A and B, d(I(A),I(B)) = d(A,B). Hence, we need only prove closure and the inverse property for the set of isometries under composition.
      Let f and g be isometries of a plane. Let A and B be two distinct points. Denote g(P) = P' and (f o g)(P) = P". Since g is an isometry, AB = A'B'. Since f is an isometry, A'B' = A"B". Hence, AB = A"B". Therefore, f o g is an isometry. Hence, the set of isometries under composition satisfies the closure property.
      Let f  be an isometry of the plane. Let A and B be two distinct points. Since f is a transformation, f has an inverse f ¹. Let C = f ¹(A) and D = f ¹(B). Since f is an isometry, d(f ¹(A), f ¹(B)) = d(C,D) = d(f(C), f(D)) = d(A,B). Hence, f ¹ is an isometry. Thus the set of isometries under composition satisfies the inverse property.
      Therefore, the set of isometries of a plane is a group under composition.//

        Several natural questions arise: Can an isometry be determined from several points? If yes, how many points are needed to determine an isometry? Is the determined isometry unique?
        Since congruence is an invariant property and three congruent corresponding sides form congruent triangles, it seems reasonable to conjecture that two pairs of three noncollinear points that determine congruent triangles could be used to determine a unique isometry. We begin to answer the question with the following theorem, which is important in proving the uniqueness of the isometry.

Theorem 3.9. An isometry of a Euclidean plane that maps each of three noncollinear points to itself is the identity transformation.

Proof.  Let A, B, and C be distinct noncollinear points, and 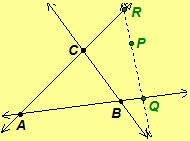let f be an isometry such that f(A) = A, f(B) = B, and f(C) = C. (We desire to show that f must be the identity transformation.) Let P be any point in the Euclidean plane distinct from A, B, and C. We need to show that f(P) = P. Either P is on one of the lines or not on any of the lines determined by A, B, and C.  
        Assume P is on one of the lines  then the ruler postulates, Theorem 3.1, and Corollary 3.4 imply f(P) = P. (The details of the proof are left as an exercise, Exercise 3.33.)
        Assume P is not on any of the three lines determined by A, B, and C. Let Q be a point on ray  distinct from A and B. By the Euclidean Parallel Postulate, line  cannot be parallel to both lines  Suppose line  intersects line  at a point R. Since Q and R are on lines , respectively, the first case implies f(Q) = Q and f(R) = R. The result, f(P) = P, follows from the first case, since P is a point on the line  The proof of remaining case is similar. Hence, f maps every point in the Euclidean plane to itself. Therefore, the isometry is the identity transformation.//

Corollary 3.10. An isometry of a Euclidean plane is uniquely determined by two pairs of three noncollinear points that determine congruent triangles.

Exercise 3.24.  Which of the following transformations are isometries? Justify.

1.  such that .

2.  such that .

3.  such that .

4.  such that .

5.  such that .

6. Let P be a point in a plane S. Define  by f(P) = P and f(Q) to be the midpoint of  for any point .

Exercise 3.25. Show that collinearity in a Euclidean plane is not necessarily invariant under a transformation. (Hint. Consider  such that .)

Exercise 3.26. Prove congruence (as defined above) is an equivalence relation.

Exercise 3.27. Prove. If  then AB = CD.

Exercise 3.28. Prove. Assume f is an isometry. If  then  

Exercise 3.29. Prove Corollary 3.2.

Exercise 3.30. Prove Corollary 3.4.

Exercise 3.31. Prove Corollary 3.5.

Exercise 3.32. Prove Corollary 3.7.

Exercise 3.33. Fill in the details for the first case in the proof of Theorem 3.9, that the ruler postulates, Theorem 3.1, and Corollary 3.4 do imply f(P) = P.

Exercise 3.34. Prove Corollary 3.10. (Show both existence and uniqueness of the isometry.)