Readings for Session 5 – (Continued)  

Intersection of Sets

  

          Before continuing reading this session, you may want to review the mathematical definitions for the words and and or covered later in this session. 

Intersection:  The set operation intersection takes only the elements that are in both sets.  The intersection contains the elements that the two sets have in common.  The intersection is where the two sets overlap.   

In set-builder notation, A ∩ B = {x ∈ U : x ∈ A and x ∈ B}.  

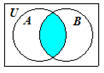
The Venn diagram for A ∩ B is shown to the right where the shaded region represents the set A ∩ B.

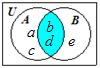
Example:   Let A = {a, b, c, d} and B = {b, d, e}.  Then A ∩ B  = {b, d}.
The elements b and d are the only elements that are in both sets A and B.
                                        

Example:  Let G = {t, a, n} and H = {n, a, t}. Then G ∩ H = {a, n, t}.   Note that here G = H = G ∩ H. 

Example:  Let C = {2, 6, 10, 14, …} and D = {2, 4, 6, 8, …}.    Then C ∩ D = {2, 6, 10, 14, …} = C. 

 

Example:  Why is the location where a street and an avenue cross called an intersection? The location is contained in both the street and the avenue. 

Example:  Let E = {d, a, y} and F = {n, i, g, h, t}.  Then E ∩ F = ∅.

 

Note:  In all the examples, the intersection is a subset of each set forming the intersection,  i.e., A ∩ B ⊆ A and A ∩ B ⊆ B. 

Disjoint Sets:  Two sets whose intersection is the empty set are called disjoint sets. 

Example:  Let E = {d, a, y} and F = {n, i, g, h, t}.  Since E ∩ F = ∅, the sets E and F are disjoint sets.  

 

      

Return to Peil's Homepage | Minnesota State University Moorhead | Mathematics Department