Readings for Session 5 – (Continued)  

Properties of Union and Intersection of Sets

 

         The following set properties are given here in preparation for the properties for addition and multiplication in arithmetic. Note the close similarity between these properties and their corresponding properties for addition and multiplication.

 
Commutative Properties:  The Commutative Property for Union and the Commutative Property for Intersection say that the order of the sets in which we do the operation does not change the result.

 

General Properties:  A ∪ B = B ∪ A               and               A ∩  B = B ∩ A.

         

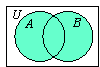
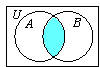
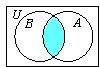
Example:  Let A = {x : x is a whole number between 4 and 8} and B = {x : x is an even natural number less than 10}.

                 Then    A ∪ B = {5, 6, 7} ∪ {2, 4, 6, 8} = {2, 4, 5, 6, 7, 8} = {2, 4, 6, 8} ∪ {5, 6, 7} = B ∪ A

                 and      A ∩ B = {5, 6, 7} ∩ {2, 4, 6, 8} = {6} = {2, 4, 6, 8} ∩ {5, 6, 7} = B ∩ A.

 

Associative Properties:  The Associative Property for Union and the Associative Property for Intersection says that how the sets are grouped does not change the result.

General Property:  (A ∪ B) ∪ C = A ∪ (B ∪ C) and (A ∩ B) ∩ C = A ∩ (B ∩ C)

 

Example:  Let A = {a, n, t}, B = {t, a, p}, and C = {s, a, p}.

                Then    (A ∪ B) ∪ C = {p, a, n, t} ∪ {s, a, p} = {p, a, n, t, s} = {a, n, t} ∪ {t, a, p, s} = A ∪ (B ∪ C)

                and      (A ∩ B) ∩ C = {a, t} ∩ {s, a, p} = {a} = {a, n, t} ∩ {a, p} = A ∩ (B ∩ C).

Identity Property for Union: The Identity Property for Union says that the union of a set and the empty set is the set, i.e., union of a set with the empty set includes all the members of the set. 

General Property:  A ∪ ∅ = ∅ ∪ A = A

Example:  Let A = {3, 7, 11} and B = {x : x is a natural number less than 0}.
                 Then A ∪ B = {3, 7, 11} ∪ { } = {3, 7, 11}.

         The empty set is the identity element for the union of sets. What would be the identity element for the addition of whole numbers? What would be the identity element for multiplication of whole numbers?

 Intersection Property of the Empty Set: The Intersection Property of the Empty Set says that any set intersected with the empty set gives the empty set. 

General Property:  A ∩  ∅ = ∅ ∩ A = ∅.

Example:  Let A = {3, 7, 11} and B = {x : x is a natural number less than 0}.
                 Then A ∩ B = {3, 7, 11} ∩ { } = { }.

        What number has a similar property when multiplying whole numbers? What is the corresponding property for multiplication of whole numbers?

Distributive Properties: The Distributive Property of Union over Intersection and the Distributive Property of Intersection over Union show two ways of finding results for certain problems mixing the set operations of union and intersection. 

General Property:   A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) and A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Example: Let A = {a, n, t}, B = {t, a, p}, and C = {s, a, p}. Then

               A ∪ (B ∩ C) = {a, n, t} ∪ {a, p} = {p, a, n, t} = {p, a, n, t} ∩ {p, a, n, t, s} = (A ∪ B) ∩ (A ∪ C)

               A ∩ (B ∪ C) = {a, n, t} ∩ {t, a, p, s} = {a, t} = {a, t} ∪ {a} = (A ∩ B) ∪ (A ∩ C)

           

       

Return to Peil's Homepage | Minnesota State University Moorhead | Mathematics Department