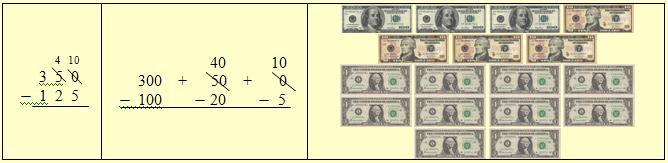Readings for Session 8 – (Continued)  

Standard Subtraction Algorithm

        We motivate the standard subtraction algorithm with both the set model and expanded notation.

Example:  Consider the problem 40 – 7.

We are unable to remove $7 from $40 without exchanging a $10-bill because there are no $1-bills to remove.  In the symbolic form, we cannot take 7 ones from 0 ones because we are unable to remove elements from an empty set.

We exchange a $10-bill for 10 $1-bills. In symbolic form, we exchange one ten for ten ones.

We remove 7 $1-bills. In symbolic form, we subtract 7 ones from ten ones.

Example:  Consider the problem 350 – 125.

We are unable to remove $5 from $350 without exchanging a $10-bill because there are no $1-bills to remove.  In the symbolic form, we cannot take 5 ones from 0 ones because we are unable to remove elements from an empty set.

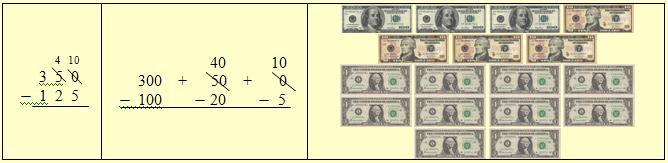
We exchange a $10-bill for 10 $1-bills. In symbolic form, we exchange one ten for ten ones.

We remove 5 $1-bills, 2 $10-bills, and 1 $100-bill. In symbolic form, we subtract five ones from ten ones, two tens from four tens, and one hundred from three hundreds.

Example:  Consider the problem 500 – 375.

Regrouping is necessary in this problem in both the ones’ and tens’ columns.

We exchange a $100-bill for 10 $10-bills and then exchange 1 $10-bill for 10 $1-bills. In symbolic form, we exchange one hundred for ten tens, and then exchange one ten for ten ones.

We remove 5 $1-bills, 7 $10-bills, and 3 $100-bills. In symbolic form, we subtract 5 ones from ten ones, 7 tens from 9 tens, and 3 hundreds from 4 hundreds.

        Try this subtraction problem by first showing the expanded notation and then the short cut form. Be sure you understand the reasoning behind the regroupings. Problem: 802 – 548.

    

      

Return to Peil's Homepage | Minnesota State University Moorhead | Mathematics Department