Decimal Multiplication and Division

Standard Division Algorithm for Decimals

Why do We Move the Decimal Points when Dividing Decimals?

The rule for decimal arithmetic says that to divide by a decimal, you "move the decimal point of the divisor (outside number) to the end of the numeral and then move the decimal point of the dividend (inside number) the same number of positions (the same distance and direction)."

Example:

Once again, this is really just a short cut for what happens when we work the problem in its fraction form.

Example: 4.5 ÷ 0.25 in common fraction form is

.

Another way to look at the division rule is to think of the decimal division as multiplying the numerator and denominator by the same power of ten.  

Example: Divide 125.46 ÷ 20.5.

Note that this may be written as eithe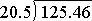r or 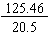. Eliminating the decimals in the denominator of the fraction form, we obtain

.

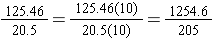So, in the standard division form, we would have

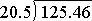or .

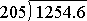Note that we multiplied the divisor and dividend both by the same value 10. When completing the division be very careful with the place value in the quotient.

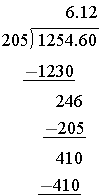
We only need to get the divisor in the form of a whole number. It is easy enough to work with a decimal in the number being divided as long as we are dividing by a whole number.

However, we would still get the correct answer if we multiplied both the divisor (denominator) and dividend (numerator) by a value that would make both the divisor and the dividend a whole number. For example, in the previous problem we could have multiplied by both the divisor and dividend by 100 and then the entire problem would have become a whole number problem, but it would have exactly the same answer as before.

Example:   We redo the previous example, 125.46 ÷ 20.5.

Eliminating the decimals in the fraction form, we obtain .

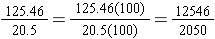So, in the standard division form, we would have

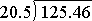or

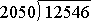
Note that we multiplied the divisor and dividend both by the same value 100. When completing the division be very careful with the place value in the quotient.

Notice that this second method of eliminating all the decimal points may make the divisor much larger, which often leads to a greater chance of an error. That is why it is best to use the standard algorithm of making just the divisor a whole number.

Self-Check Problem

A meat market has 38.25 pounds of hamburger to be wrapped into 2.25 pound packages. How many packages of meat can they wrap?

Solution

return to top | previous page | next page