Reading and Writing Percents

Rewriting Fractions as Percents

There are two common ways to translate a fraction into a percent:

(1) convert to an equivalent fractions with a denominator of 100, or

(2) use the division interpretation of the fraction.

Fractions that have denominators that are factors of 100 can be rewritten with a denominator of 100 and are easy to translate into percents by using the definition of percent. All we need to do is to convert to the equivalent fraction that has 100 as a denominator.

Examples: Convert seven hundredths, one-half, and one-fourth to percents.

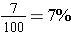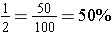, , and

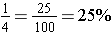
This works well for fractions that are easy to convert to fractions with denominators of 100, but the division interpretation of fractions would probably work better for most fractions.

Terminating Decimals to Percents

Fractions that have denominators that are not factors of 100 are best converted to their decimal form before finding the equivalent percent. When the decimal equivalent is a terminating decimal, we can find the percent by "reading it off at the hundredths place".

Example: Convert one-eighth to a percent.

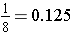
How many hundredths is this?

Since the hundredths place value is the second decimal place behind the decimal point, we read 0.125 as  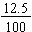 which in turn can be written as 12.5%. This is where the infamous "move the decimal point 2 places" rule comes from. What we are really doing is reading the decimal value at the hundredths place value.

Repeating Decimals to Percents

As we have seen before, many fractions do not terminate. For example, the fraction 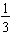has a repeating decimal form 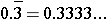. The exact percent equivalent for 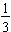is 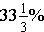. We see this by looking at 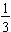and how it is divided into a decimal form where we write the remainder of the hundredths position as a fraction.  

We usually do not write percents as repeating decimals. We either write them with a fractional part of a percent or we round it to a certain decimal position. This rounding is what causes the common misconception that

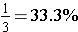
or just 33%. The common fraction  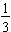is approximately equal to 33.3% written as .  

Exact or Approximate?

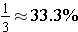The fraction 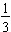is exactly equal to 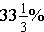.   In this class, unless otherwise stated give the exact amount; you must give the percent that is exactly equal to the amount given.

When working application problems, approximations may be used, but be sure that you use a symbol that states that your answer is an approximation. Use either the symbol ≈ or for "approximately equal to".   Your instructor will tell you which symbol the instructor wants you to use.

For more discussion on approximations and rounding see Session 28.

Self Check Problems

Convert each fraction to a percent.

	Solution
	Solution
	Solution
	Solution

Joke or Quote

A parent was complaining to the stock broker. "I have spent nearly $20,000 on my child's education. And here Dana goes and marries someone with an income of only $1400 a year."

"Well," replied the broker, "that's a seven percent return on your investment. What more can you expect in these times?"

return to top | previous page