Introduction to Integers

Integers, Absolute Value, and Additive Inverse

Additive Inverse (Inverse Property for Integer Addition)

We generalize the relationship where opposites of the same absolute value cancel each other out. We further illustrate with examples with both models.

3 + (–3) = 0	–5 + 5 = 0
Beginning at zero, in the measurement model, a move of three units to the right followed by three units to the left brings us back to zero.	Beginning at zero, in the measurement model, a move of five units to the left followed by five units to the right brings us back to zero.

We notice that the result of combining a number and its opposite is zero. This motivates the following formal definition.

Additive Inverse: For every integer n, there is a unique integer m such that n + m = m + n = 0.

The integer m is called the additive inverse of n.

This property of integers is called the inverse property for integer addition.

Examples: Find the additive inverse for each of the following integers.

Integer	7	–5	–13	29	0
Additive Inverse	Inverse	Inverse	Inverse	Inverse	Inverse

If we consider the negative sign as representing the opposite, the above example illustrates that –(–5) = 5 and –(7) = –7, i.e. the opposite of an integer is equivalent to the additive inverse of the integer. This relationship allows us to give an algebraic definition for absolute value.

Algebraic Definition of Absolute Value:

The absolute value of a is defined by .

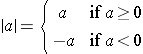Examples:

(a) |5| = 5 since 5 > 0.

(b) |–5| = –(–5) = 5 since –5 < 0.

(c) |18| = 18 since 18 > 0.

(d) |–24| = –(–24) = 24 since –24 < 0.

Self Check Problems

Integer	7	–4	–13	29	0
Absolute Value	Solution	Solution	Solution	Solution	Solution

 

return to top | previous page | next page