TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

            3.6.1 Similarity Transformations  Printout
In the physical world, one cannot increase the size or quantity of anything without changing its quality. Similar figures exist only in pure geometry.
—Paul Valéry (1871–1945)

        The concept of similar triangles and similar figures is an important component of Euclidean geometry. Many applications for the geometric properties of similarity are used. The use of scale drawings such as maps and blueprints are important in travel and construction. The use of triangulation properties are important in navigation and measuring distances indirectly. The right triangle trigonometry definitions for sine, cosine, and tangent are all based on the properties of similar triangles. In this section, we define the concept of similarity in terms of transformation.

Definition.  The transformation f of a plane onto itself is a similarity with ratio r if there is a nonzero real number r such that for any two points A and B where A' =f(A) and B' = f(B), d(A',B') = |r|d(A,B).  The number r is called the ratio of the similarity.

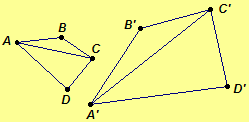     Note a similarity with ratio r = -1 or r = 1 is an isometry. We would expect many of the same theorems for isometries should hold for similarities, which they do. Most of the proofs require a few minor adjustments that generalize for the scale factor r. Here, we prove one of the theorems (betweenness of points is invariant) to illustrate one such modification and leave most of the proofs of the other theorems to the reader. In hyperbolic geometry and elliptic geometry, similar triangles are congruent triangles. Therefore, proving the theorems for a neutral geometry provides little, if any, additional information.

Exercise 3.86.  (a) Determine the inverse of a similarity with ratio r. (b) Determine the ratio of the composition of a similarity with ratio r₁ and a similarity with ratio r₂.

Theorem 3.29. The set of all similarities of a plane is a group under composition.

Theorem 3.30. Betweenness of points is invariant under a similarity of a neutral plane.

Proof.  Let f  be a similarity with ratio r of a neutral plane. Let A, B, and C be three distinct points such that B is between A and C. Further, let A' = f(A), B' = f(B), and C' = f(C). By the definition of betweenness of points, AC = AB + BC and {A, B, C} is collinear. Since f is a similarity, A'C' = |r|(AC), A'B' = |r|(AB), and B'C' = |r|(BC). Hence, A'C' = |r|(AC) = |r|(AB + BC) = |r|(AB) + |r|(BC) = A'B' +B'C'. Thus, by the Triangle Inequality, {A', B', C'} is collinear. Therefore, B' is between A' and C'.//

Corollary 3.31. Collinearity is invariant under a similarity of a neutral plane.

Corollary 3.32. The image of a line segment under a similarity with ratio r of a neutral plane is a line segment where the length of the image is r times the length of the segment.

Corollary 3.33. The image of a triangle under a similarity of a Euclidean plane is a similar triangle.

Corollary 3.34. Angle measure is invariant under a similarity of a Euclidean plane.

Corollary 3.35. The image of a circle under a similarity of a neutral plane is a circle.

             We wrote a more general definition of congruency based on results and investigation with isometries. An analogous definition may be formed for sets of points being similar. The above results imply a more general definition for similarity for any two sets of points, which would include all figures under one definition.

Definition.  Two sets of points are said to be similar provided there is a similarity where one set is the image of the other set. Write  if and only if there is a similarity f such that .

Theorem 3.36. A similarity of a Euclidean plane is uniquely determined by three noncollinear points and their images.

Exercise 3.87. Find the ratio of similarity if a 4 centimeter segment has a 6 centimeter image.

Exercise 3.88. Find the length of the image of an 8 centimeter segment under a similarity with a ratio of 3/4.

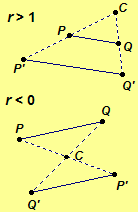
Definition. A dilation with center C and ratio r, denoted H_C,r, is a transformation of a plane where H_C,r(C) = C and if P is distinct from C, then P' = H_C,r(P) such that C, P, and P' are collinear and d(C,P') = |r|d(C,P). Further, if r < 0, then P'-C-P; if 0 < r < 1, then C-P'-P; and if r > 1, then C-P-P'.  A dilation is also called a homothety.

Exercise 3.89.  Draw a right triangle  with right angle at C. Accurately draw the triangle's image under each dilation H_O,2, H_O,–2, and H_O,1/2.

      (a)  O = C

      (b)  O = A 

      (c)  O is the midpoint of

      (d)  O is a point in the exterior of  

Exercise 3.90.  Draw the image of each dilation H_C,2, H_C,–2, and H_C,1/2.

 
Click here to investigate dynamic illustrations of the above diagram GeoGebra or JavaSketchpad.

Theorem 3.37. A dilation with center C and ratio r of a Euclidean plane is a similarity with ratio r.

Proof.  Let H_C,r be a dilation with center C and ratio r and let X' = H_C,r(X) for any point X. Let P and Q be two distinct points. We need to show that P'Q' = |r|(PQ). The equality is clearly true, if C is either P or Q. Therefore, we assume C, P, and Q are distinct. Hence, either C, P, and Q are collinear or C, P, and Q are noncollinear.
      Case 1. Assume C, P, and Q are collinear. We show the case where r > 1 and P is between C and Q, the other cases are similar. By the definition of a dilation, we have C-P-P' and C-Q-Q'. Hence, all the points C, P, P', Q, and Q' are collinear. Since C-P-Q and by the definition of dilation, CP' = r(CP) < r(CQ) = CQ'. Thus, since all the points are on the same side of C, we have C-P'-Q'. Hence, CP + PQ = CQ and CP' + P'Q' = CQ'. Therefore, P'Q' = CQ' – CP' = r(CQ) – r(CP) = r (CQ – CP) = r(PQ).
      Case 2. Assume C, P, and Q are noncollinear. We show the case where r > 1, the other cases are similar. By the definition of a dilation, we have C-P-P' and C-Q-Q'. Consider  and ,  and  Hence, by SAS Similarity Theorem,  Hence, P'Q' = r(PQ).
      The other cases are similar; therefore, the dilation H_C,r is a similarity.//

Corollary 3.38. The image of a segment under a dilation of a Euclidean plane is a parallel segment.

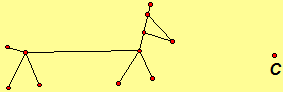
Investigation Exercise 3.91. Each of the following larger stick figures is a similarity of the smaller stick figure where one of the figures is a dilation. Draw several more of the larger stick figures on this sheet. Can you find a similarity that maps the original dilated figure to the others?

      The above exercise implies the next theorem, which gives a relationship of similarities to dilations and isometries.

Theorem 3.39. A similarity of a Euclidean plane is the composition of a dilation and an isometry.

      We state the theorem without proof since the proof is beyond the scope of this course. The proof involves results from topology.

Exercise 3.92.  How do the areas of a region and its image compare when the ratio of dilation is 2/3?

Exercise 3.93.  Find the image of the point (3,4) under a dilation with center at the origin and ratio of –5/3.

Exercise 3.94.  Prove Theorem 3.29.

Exercise 3.95.  Prove Corollary 3.31.

Exercise 3.96.  Prove Corollary 3.32.

Exercise 3.97.  Prove Corollary 3.33.

Exercise 3.98.  Prove Corollary 3.34.

Exercise 3.99.  Prove Corollary 3.35.

Exercise 3.100.  Prove Theorem 3.36.

Exercise 3.101.  Prove the cases where r < 0 for Theorem 3.37.

Exercise 3.102.  Prove Corollary 3.38.