Solution Basic Theorems Exercise 4.3.
Prove Theorem 4.3.
If you think you can or can't, you are right.
—Henry Ford (1863–1947)

Important Note. You may have a different proof, which may be more "elegant" than the sample solution that follows. But you must begin the proof by assuming a given arbitrary line. Also, you may not assume the line has any points. You must prove the existence of all three points.

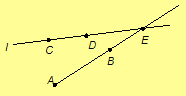
Theorem 4.3. Every line is incident with at least three distinct points.

Proof.  Let l be a line. By Axiom 3, there exist four points A, B, C, and D, no three of which are collinear. Hence at least two of the points, say A and B, are not on l. By Axiom 1, line AB exists. By Axiom 2, there is a point E incident with l and AB. Also, note E is neither C nor D, since no three of A, B, C, and D collinear. Then one of three cases is true: (1)  C and D are both on l. (2) Only one of C or D is on l. (3) Neither C nor D is on l.
        If C and D are both on l, then E, C and D are three distinct points on l.
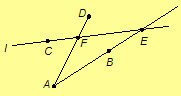
        Assume only one of C or D is on l; without loss of generality, say C is on l. By Axioms 1 and 2, there is a point F on l and AD. Note F cannot be E, since A, B, and D are noncollinear. Also, F cannot be C, since A, C, and D are noncollinear. Hence l is incident with distinct points C, E, and F.
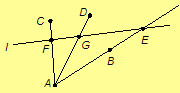
        Assume neither C nor D is on l. There is a point F on l and AC and a point G on l and AD, by Axioms 1 and 2. Note E, F, and G are distinct, since no three of A, B, C, and D collinear. Hence l is incident with distinct points E, F, and G.
        Therefore, by the three cases, l is incident with at least three distinct points.  //