TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

          4.2.1 Axioms and Basic Definitions for Plane Projective Geometry  Printout
Teachers open the door, but you must enter by yourself.
—Chinese Proverb

Undefined Terms. point, line, incident

Axiom 1. Any two distinct points are incident with exactly one line.

Axiom 2. Any two distinct lines are incident with at least one point.

Axiom 3. There exist at least four points, no three of which are collinear.

Axiom 4. The three diagonal points of a complete quadrangle are never collinear.

Axiom 5. (Desargues' Theorem) If two triangles are perspective from a point, then they are perspective from a line.

Axiom 6. If a projectivity on a pencil of points leaves three distinct points of the pencil invariant, it leaves every point of the pencil invariant.

Basic Notation.

• Points are denoted by upper case letters and lines by lower case letters.
• Denote the line determined by two distinct points A and B by AB.
• Denote a point determined by two distinct lines a and b by a · b. Note that this refers to the point of intersection of two lines, not the set of points of intersection, i.e. a ∩ b = {a · b}.

Basic Definitions.

• A set of points is collinear if every point in the set is incident with the same line.
  Points incident with the same line are said to be collinear.
   
• Lines incident with the same point are said to be concurrent.
   
• A complete quadrangle is a set of four points, no three of which are collinear, and the six lines incident with each pair of these points. The four points are called vertices and the six lines are called sides of the quadrangle.
  Example: Complete quadrangle ABCD has vertices A, B, C, and D. The sides are AB, AC, AD, BC, BD, and CD.
   
• Two sides of a complete quadrangle are opposite if the point incident to both lines is not a vertex.
  Example: Complete quadrangle ABCD has three pairs of opposite sides AB and CD, AC and BD, and AD and BC.
   
• A diagonal point of a complete quadrangle is a point incident with opposite sides of the quadrangle.
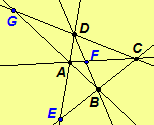  Model. The vertices of the quadrangle ABCD are A, B, C and D. The sides of the quadrangle are AB, AC, AD, BC, BD, and CD. The opposite sides are AB and CD, AC and BD, and AD and BC. The diagonal points of the quadrilateral are E, F and G.

Click here to go to a dynamic illustration of a quadrangle GeoGebra or JavaSketchpad.

 

• A triangle is a set of three noncollinear points and the three lines incident with each pair of these points. The points are called vertices, and the lines are called sides.
  Cautionary Note.  A triangle in a projective geometry is different from a triangle in Euclidean geometry. Each side of a triangle in projective geometry is a line, whereas each side of a triangle in Euclidean geometry is a segment. Betweenness of points in projective geometry is not defined; therefore, projective geometry does not have segments defined. In spite of this, we will often use Euclidean triangles in illustrations.
   
• Two figures are perspective from a point provided the lines determined from corresponding points are concurrent. The point is called the center. 
• Two figures are perspective from a line provided the points of intersection of corresponding sides are collinear. The line is called the axis.
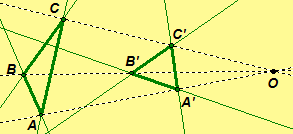
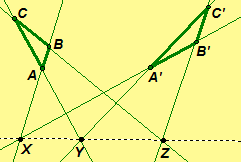
  Examples: The left-hand figure illustrates triangles perspective from a point. (The lines AA', BB', and CC' are concurrent through O.) The right-hand figure illustrates triangles perspective from a line. (The lines AB and A'B' intersect at X, AC and A'C' intersect at Y, and BC and B'C' intersect at Z; further, X, Y, and Z are collinear.)

                     
Click here for a dynamic illustration of perspective from a point and perspective from a line  GeoGebra or JavaSketchpad.

• A set of points incident with a line is called a pencil of points (or range of points), and the line is called the axis. A set of lines incident with a point is called a pencil of lines, and the point is called the center.
  Example: A set of points {A, B, C, D} on a line l is called a pencil of points with axis l. A set of lines {a, b, c, d} concurrent at a point P is called a pencil of lines with center P.

• A one-to-one mapping between two pencils of points is called a perspectivity if the lines incident with the corresponding points of the two pencils are concurrent. The point where the lines intersect is called the center of the perspectivity. A perspectivity is denoted
  
   where O is the center of perspectivity.
• A one-to-one mapping between two pencils of points is called a projectivity if the mapping is a composition of finitely many perspectivities. A projectivity is denoted
  
  .
  
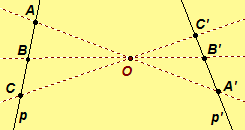
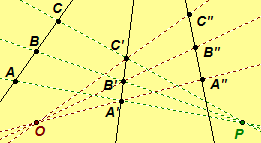
  Examples: The left-hand figure is a perspectivity between two pencils of points with axes p and p',
  
  , and the right-hand figure is a projectivity,
  
  , consisting of the product of two perspectivities,
  
   and
  
   
  Click here for a dynamic illustration of the perspectivity and projectivity. GeoGebra or JavaSketchpad.