Solution Basic Theorems Exercise 4.4.
Prove Theorem 4.4.
Failure is instructive. The person who really thinks learns quite as much from his failures as from his successes.
—John Dewey (1859–1952)

Important Note. You may have a different proof, which may be more "elegant" than the sample solution that follows.

Theorem 4.4. Every line is incident with at least four distinct points.

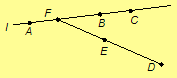
Proof.  Let l be a line. By Theorem 4.3, there are three distinct points A, B, and C on l. By Axiom 3, there exist two distinct points D and E not on l where no three of D, E and two of A, B and C are collinear. Without loss of generality, assume no three of B, C, D, and E are collinear. By Axiom 1 and its dual (Theorem 4.1), there is a point F = l · DE. Also, note F is neither B nor C, since no three of B, C, D, and E collinear. We have two cases: either F = A or F is distinct from A.
        If F is distinct from A, then l is incident with the four distinct points F, A, B, and C.
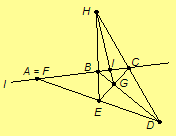
        Assume F = A. There is a point G = BD · CE, by Axiom 1 and its dual. We assert that G is not on l. Suppose G is on l, then by Axiom 1 BC = l = BG = BD. But this contradicts that B, C, and D are noncollinear. Hence G is not on l. By a similar argument there is a point H = BE · CD, H is not on l, and H is distinct from G. By Axioms 1 and its dual, there is a point I = GH · l. Note I, G and H are collinear. We assert that I cannot be A = F. Suppose I = A = F. By Axiom 1, its dual and the definition of a complete quadrangle, BCDE is a complete quadrangle with diagonal points I = F = BC · DE, G = BD · CE and H = BE · CD. By Axiom 4, the diagonal points I, G, and H are noncollinear, but this contradicts that  I, G, and H are collinear. Thus A, B, C, and I are distinct points on l.
        Therefore, l has at least four distinct points. //