TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

             2.7.2 Hyperbolic Parallel Postulate  Printout
Out of nothing I have created a strange new universe.
 —János Bolyai (1802–1860)

 

Hyperbolic Parallel Postulate. Through a point not on a line there is more than one line parallel to the given line.

      As with the Euclidean Parallel Postulate, there are many statements that are equivalent to the Hyperbolic Parallel Postulate. A sample list is given below. Note the similarity to the equivalent Euclidean postulates; from this pattern we should be able to see many other equivalent statements. The Poincaré Half-plane is a model of a hyperbolic geometry, with which we have completed several examples in previous sections. The Poincaré Disk is another model of a hyperbolic geometry. Click here for a illustration of the Poincaré Disk or investigate the Poincaré Disk with interactive java software NonEuclid. This survey course will not develop or prove any of the concepts in hyperbolic geometry. The exercises below are meant to explore basic principles, without proof. Many books on non-Euclidean geometry thoroughly develop the concepts of hyperbolic geometry, see those for proofs.

Hyperbolic Proposition 2.1. The sum of the measures of the angles of a triangle is less than 180.

Hyperbolic Proposition 2.2. Similar triangles are congruent triangles.

Hyperbolic Proposition 2.3. Through a given point not on a line there are infinitely many lines parallel to the given line.

Hyperbolic Proposition 2.4. The summit angles of a Saccheri quadrilateral each measure less than 90.

Hyperbolic Proposition 2.5. No quadrilateral is a rectangle.

Use dynamic geometry software with the Poincaré Half-plane for the construction investigations (Geometer's Sketchpad, GeoGebra, or NonEuclid). The script for Geometer's Sketchpad or GeoGebra Poincaré Half-plane is in Appendix B of the Title Page and Index. Make sure you use the Poincaré Half-plane construction tools for lines, rays, segments, angles, circles, etc. Do not use the Euclidean tools.

Exercise 2.68.  Construct a triangle in the Poincaré Half-plane. (a) Find the sum of the measures of the angles.  (b) Find a triangle where the sum of the measures of the angles is less than 5.  (c) Find a triangle where the sum of the measures is more than 175.

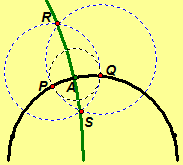
Exercise 2.69. (a)  Construct two perpendicular lines in the Poincaré Half-plane, as illustrated on the right. (b) Prove the two lines are perpendicular.  (c) Is this construction valid for a neutral geometry (or Euclidean geometry)? Explain.

Exercise 2.70. Use the procedure from Exercise 2.69 for this exercise. (a) Construct a Saccheri quadrilateral in the Poincaré Half-plane that has the base and sides all congruent. (b) May we say that in a hyperbolic world, "No body is a 'square'."? Explain.

Exercise 2.71.  (a) Construct a quadrilateral in the Poincaré Half-plane that has three right angles. (This quadrilateral is called a Lambert quadrilateral after Johann Lambert (1728–1777).)  (b) What is the measure of the fourth angle?  (c) Prove or disprove that a Lambert quadrilateral is a parallelogram.  (d) Is the result of part (c) valid for a neutral geometry (or Euclidean geometry)?

Exercise 2.72.  (a) Construct two parallel lines in the Poincaré Half-plane by constructing them perpendicular to the same line. (b) What happens with the distance between the two parallel lines as you move away from the perpendicular line?

Exercise 2.73. Investigate the question: In the Poincaré Half-plane, do two parallel lines always have a common perpendicular? If they do not always have a common perpendicular, how are the two parallel lines related?

Exercise 2.74. Use the models definitions, not Geometer's Sketchpad or GeoGebra for this exercise. Given A(0, 2), B(0, 1), C , and D  in the Poincaré Half-plane.  (a) Show quadrilateral ABCD is a Saccheri quadrilateral.  (b) How do the lengths of the summit and base compare?