Ed602 Lesson 5

Assignment and Information

Reading: Chapter 4

Definition Page: Contains definitions arranged alphabetically.

Chapter 4 (lesson 5) notes and vocabulary Notes:

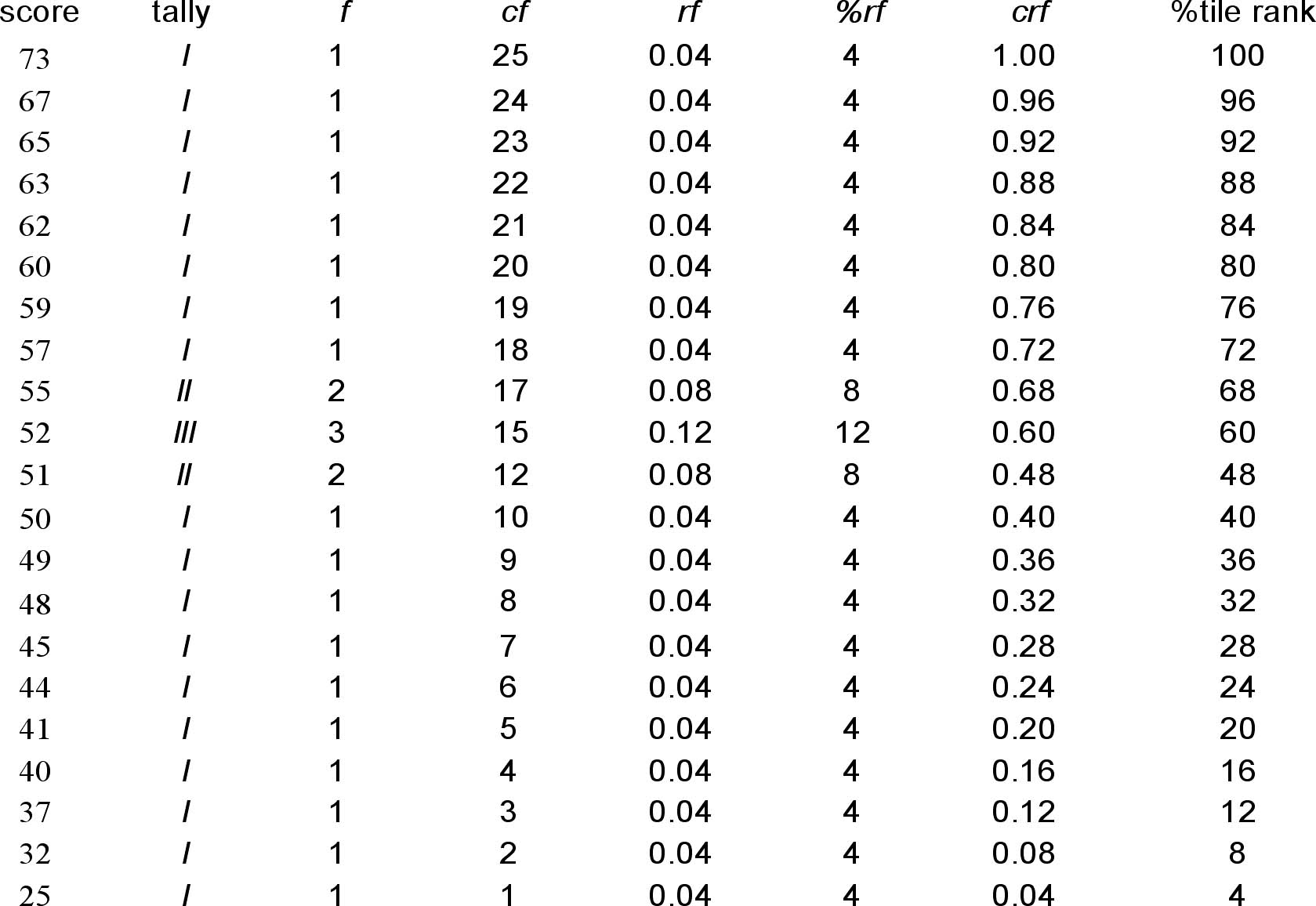Okay, now that we have collected all our BASC data, we need a way of sharing that data with the public in a way that makes sense. While frequency distributions like this one are nice, they are often too bulky for most journal publications, and they donÍt allow for easy comparisons between groups. Measures of central tendency come in handy, because they allow you to sum up an entire table of data into one score. This is an average or typical score for the group.

Mode - the most frequently occurring score in your data - For our BASC data 52 occurs the most often, three times.

The modal score is ñtypicalî because it happened the most often. If you were trying to guess someoneÍs score, you have the highest probability of being exactly right if you guess the mode as their score.
The mode provides no information about the rest of the distribution, just what score happened most
The mode can be used with all scales of measurement (nominal, ordinal, interval and ratio)
The mode is often used to report strongly bimodal data

Median - The score in the middle, when scores are ordered numerically - for our BASC data we have 25 scores, so the half way point is the 13th score. Counting down from the top, the 13th score is 52

The median score is ñtypicalî because half the scores are lower and half the scores are higher, which minimizes the distance between the median and each of the raw scores. That means that if you have to guess a score and pay a dollar for each point you are away from that score, your best bet is the median, because you will spend the least amount of money on wrong guesses that way.
The median score can be used in ordinal, interval and ratio scales, it can not be used for nominal data, because you canÍt order nominal data numerically.
The median score is less sensitive to extreme scores, or outliers, so it is often used when reporting heavily skewed data.

The text gives a formula for calculating the median for data that has tied scores around the median. This formula is often used in statistical software because it can be significant that a score is the first or 6th score in a set of tied scores (it helps in pointing out slight skew for example). It is helpful to understand this formula, but for homework purposes, our data is small enough that counting out the median score by hand is easier, and the score will make more sense to the common reader. If you want to try and calculate the median with the percentile formula for practice, you should get a median BASC score of 51.67 which reflects the fact that our median score is the first of the 3 tied scores.

Sample Mean or Mean () - The sum of the scores divided by the number of scores in the sample. For our BASC data, if you sum the scores, you should get 1285. Then divide this number by 25, since we have 25 scores, and we get a mean of 51.40.

The mean is most typical because it is the amount or score that each person would get if the scores were evened out, in other words if we were trying to be fair in giving out the same scores to everyone.
The mean can only be calculated on interval or ratio data. It does not make sense to calculate the average phone number of people in town.
The mean is sensitive to extreme scores, or outliers, so it is not good to use with heavily skewed data.
The sum of the deviations around the mean should be zero, this is a good way to check if you calculated the mean correctly. See table below.
The sum of the deviations squared (sum of squares, SS) is smaller for the mean than for any other score which will be important in later calculations. See table below.
The mean is the only measure of central tendency that uses every score in the data set, so it is usually the most representative of the data.

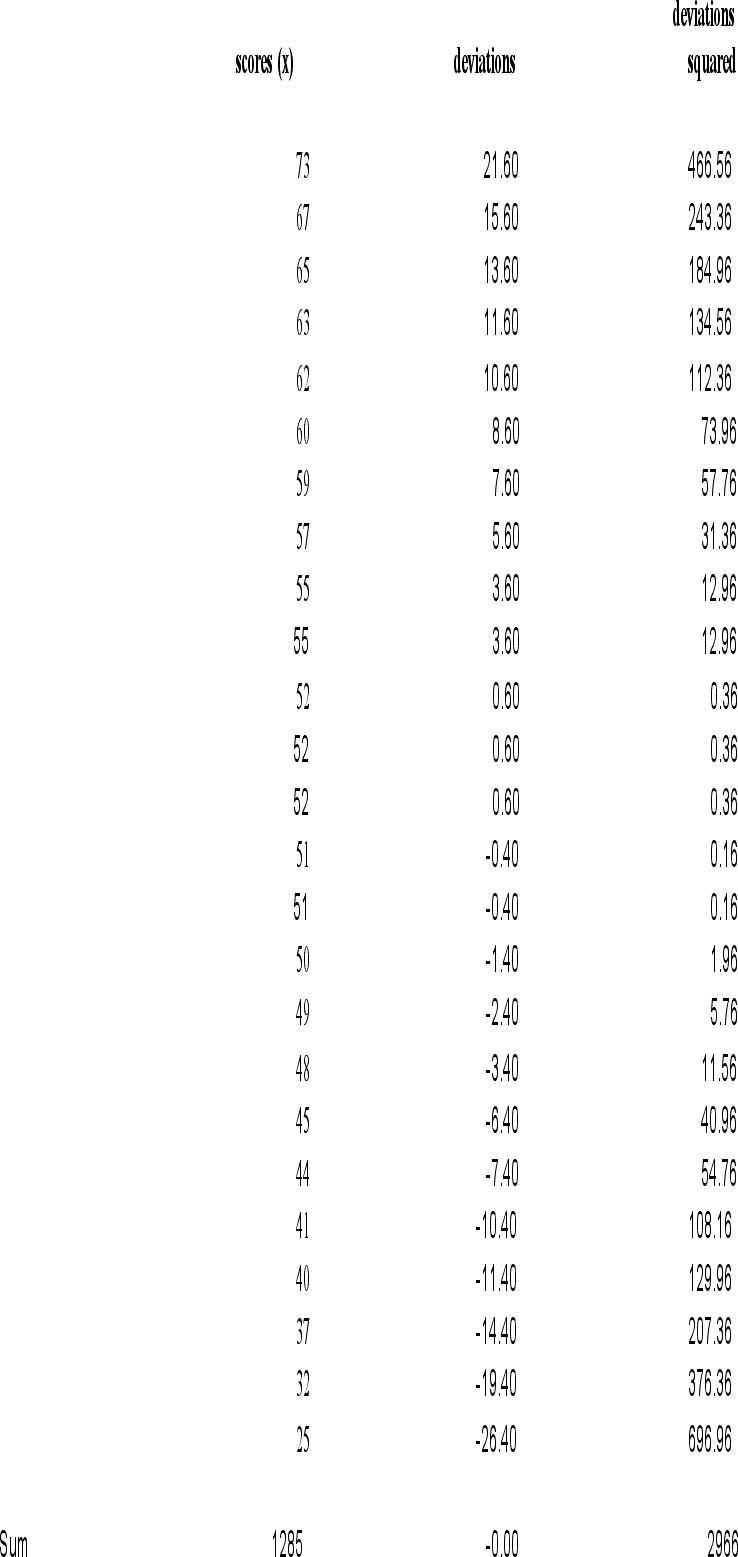Power in statistics is the ability to detect differences between groups when there actually is a difference between groups. Because the mean uses every score in the data set, it is the most statistically powerful of the three measures. Unless you have a good reason to use mode or median, like bimodal distributions or heavily skewed data, the best measure to use is the mean.

Vocabulary:

Measures of Central Tendency - Numbers that represent the average or typical score obtained from measurements of a sample. Mean, median and mode are the three most common measures of central tendency.

Measures of Variability - Numbers that indicate how much scores differ from each other and the measure of central tendency in a set of scores. These will be covered in detail in later chapters, but variance and standard deviation are two examples of measures of variability.

Mode - The most frequently occurring score in a distribution of scores. For our BASC data, the mode is 52, because there are 3 subjects who scored 52. Unimodal - a distribution with one mode. Our BASC data is unimodal. Bimodal - a distribution with two modes. Multimodal - a distribution with more than two modes.

Median - A score value in the distribution with an equal number of scores above and below it. The median is the 50th percentile in a distribution. The median for our BASC scores is also 52, because the 13th score when they are in rank order is 52.

Sample mean ( ) - The sum of a set of scores divided by the number of scores summed. In adding all our BASC scores I get 1285, then I divide by 25 (the number of scores) and I get a sample mean of 51.40.

Population mean () - The sum of all the scores in a population divided by the number of scores summed. This is the same as a sample mean, but using every score for every subject, rather than just a small sampling.

Sum of squares (SS) - A numerical value obtained by subtracting the mean of a distribution from each score in the distribution, squaring each difference, and then summing the differences. This number by itself means very little, but it is a key component of many statistical calculations.