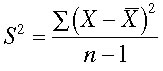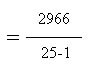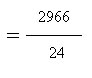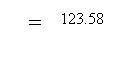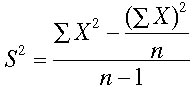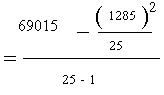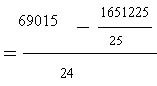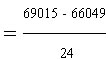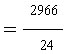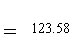Lesson - 6

.

Assignments and Information

Variability in statistics can be a double edged sword. If you are comparing two groups and there is a statistically significant difference, or variation, between those two groups, you have struck “gold”. That variation is what researchers stay up late praying to find. However, if you have a lot of variability within your groups, that can be a problem. The high variability within your groups can be like radio static, excess noise that keeps you from detecting a difference between groups.
There are several ways to report variability in a set of scores.
Range - the numerical difference between the highest and lowest scores in a distribution.
- Range is easy to compute
- Range is easy for the general public to understand
- In a normal distribution, range is related to standard deviation. The standard deviation is roughly about 1/4 of the range.
- The range can be deceptively high if there is an extreme score
- The range tends to increase as samples get larger, so it is not a good idea to compare the ranges of samples that are different sizes.
- When researchers do take the time to report the range for their data, they often just list the highest and lowest scores. Please remember that the range technically is not those scores, but the distance between the scores. Our BASC data ranged from 73 to 25, but the range of our data is 48 (73 - 25 = 48).
Interquartile Range (IQR) - the range of values of the middle 50 percent of the scores in a distribution
- IQR is often used to report ordinal data
- IQR can reduce the effects on the range of a few extreme scores
- IQR is sometimes used when reporting heavily skewed data
- We can find the IQR for our BASC data by cutting off the top and bottom six scores. This leaves us with
scores from 59 to 45, and an IQR of 14 (59 - 45 = 14).
Please note - The formula on page 79 that requires you to use a second formula on page 42 is only needed for large samples, where hand counting would be inefficient. Quite honestly, if you have that much data, you will probably have the computer run the formulas for you, anyway. Because all homework and quizzes are based on small samples, it will be easier to just count out the middle 50 percent of the scores for the IQR. Please use the hand counting method rather than the formula for all homework, quizzes, and tests.
Variance - a measure of dispersion which produces results in terms of square units, and for that reason is rarely used. However, the variance is vital to the statistical technique of ANOVA, which is covered in lesson 13.
- If you remember from chapter 4, any time we sum the deviations for a distribution of scores, we always end up with a zero, which isn’t very helpful in describing our data. To get around this problem, we squared the deviations before summing and averaging them. In this way, each set of data will have a unique score describing how much variation is in the data.
- Variance gives the measure of variation in units squared, which is hard to interpret.

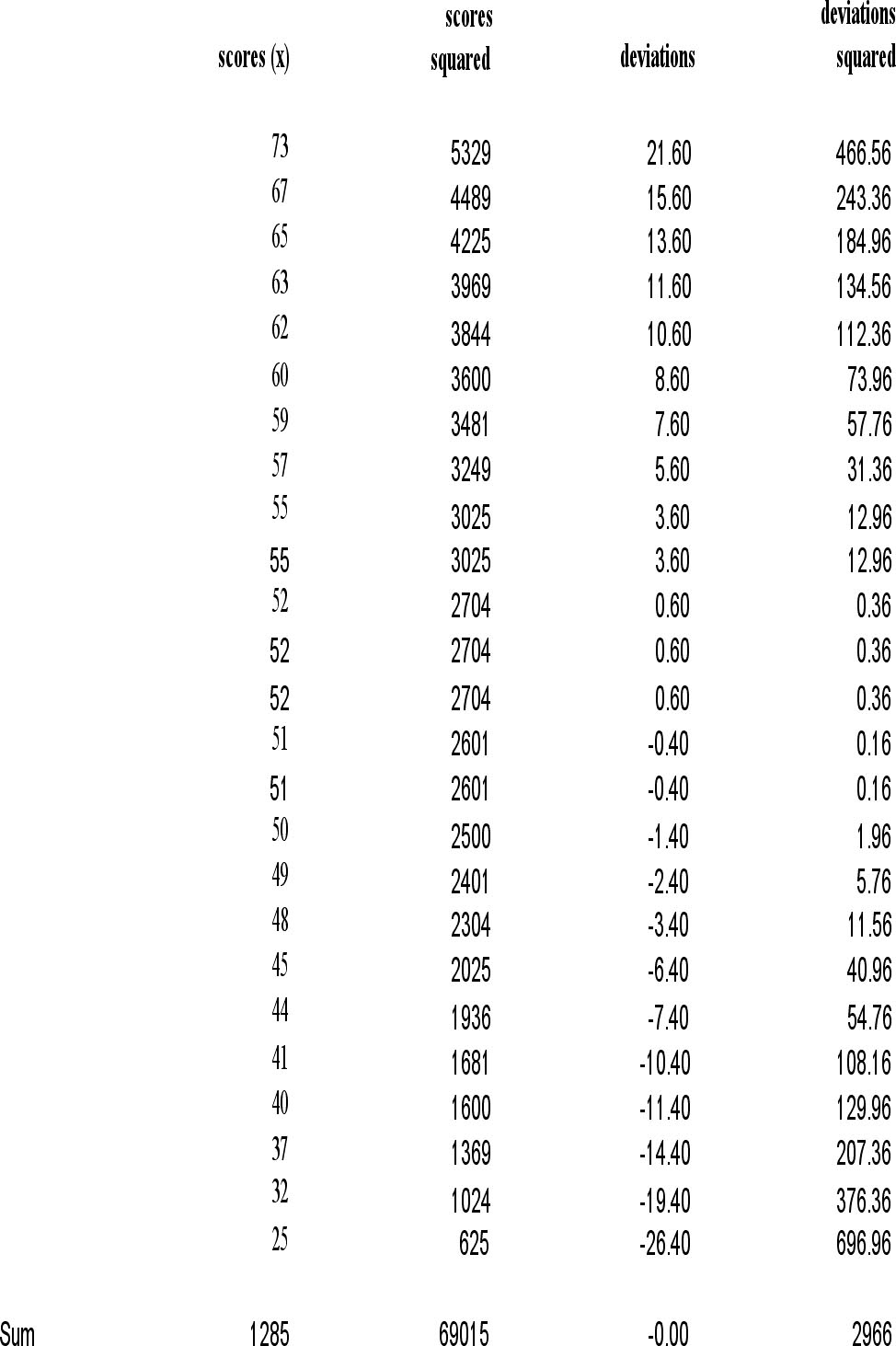
In lesson 4 we created the following table with our BASC scores
Now lets plug these numbers into the formula for estimated population variance using the definitional formula from page 82 in the text.
a) We know from the bottom of the fourth column in the table that the sum of the deviations squared (the entire numerator of our fraction) is 2966. We also know that we have an n or sample size of 25 students. b) We then simplify the denominator (25-1=24) and c) end by dividing. This gives us an estimated population variance of 123.58 square points on the BASC.We should get the same answer if we use the computational formula from page 84 in the text.
a) We take the sum on the squared scores from the bottom of the second column in our table, 69015. We get the sum of the scores from the bottom of the first column, 1285. Our n is still 25 students. b) We simplify our denominator (25 - 1 = 24) and square the 1285. c) Then we can divide the 1651225 by the 25. d) Next we subtract the 66049 from the 69015. e) finally, we divide the 2966 by the 24 to get an estimated population variance of 123.58 square points on the BASC just like the other formula.
Standard deviation - a measure of the average of how much scores in a distribution differ from the mean. - standard deviation is calculated by taking the positive square root of the variance. This gets rid of the units squared issue that makes variance hard to interpret. - standard deviation tells you how spread out your data set is. * A small standard deviation (generally less than 1/4 of your range) suggests that the scores are tightly grouped around your mean. Your mean scoreis VERY typical of your data. * A large standard deviation (generally more than 1/4 of your range) suggests that the scores are more evenly spread out across your range, so the mean score isn’t very typical of your data. * Image 1 shows a set of data with a small standard distribution, images 2 and 3 show two possible data sets with larger standard deviations. Notice that large and small standard distributions are relative terms. The standard distribution needs to be compared to the range to really be useful. is VERY typical of your data. 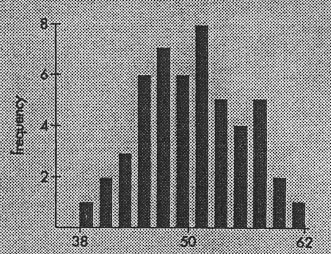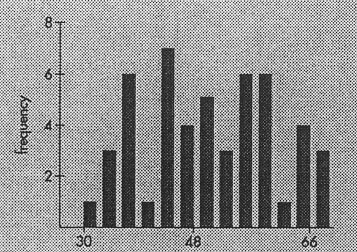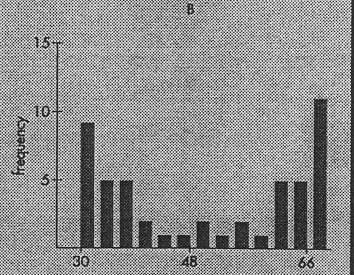* A large standard deviation (generally more than 1/4 of your range) suggests that the scores are more evenly spread out across your range, so the mean score isn’t very typical of your data. Image 1 shows a set of data with a small standard distribution, images 2 and 3 show two possible data sets with larger standard deviations. Notice that large and small standard distributions are relative terms. The standard distribution needs to be compared to the range to really be useful.
Image 1.
	mean - 50 SD - 5 range 62-38=24
Image 2.
	mean - 50 SD - 10 range 68-31 = 37
Image 3.
	mean - 4.7 SD - 1.6 range 6.8-3.0=3.8