Fraction Division

 

 Motivation Problems

Consider the following two basic problems.

Your mother told you to get $5 in quarters. How many quarters should you bring back?

Dad told you to give the chickens four pails of feed. You are only strong enough to carry half a pail at a time. How many trips do you need to make?

You would probably solve both problems in a similar manner. You would probably solve the first problem by considering that there are four quarters in a dollar. And then since you have $5 and 5 · 4 = 20, we would have twenty quarters. For the second problem, you would probably consider that there are two halves in each pail so that two trips are needed for one pail. And then since four pails of feed are needed and 4 · 2 = 8, you would need to make eight trips.

But, if we use the numbers as given in the original problems, the problems are actually division problems based on the repeated-subtraction model for division, since we are asking how many 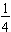dollars are needed to make $5, 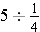(how many one-fourths are in five), and how many 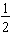  pails are needed to make 4 pails, 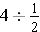(how many one-halves are in four).

We model the two problems below and write the problem in both the division and multiplication forms.

First Problem: We use a fraction strip to represent one dollar.

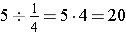
You would bring twenty quarters back.

Second Problem: Again, use a fraction strip to represent one pail.

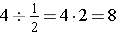
You would need to make eight trips.

Note that both of these basic problems motivate the common rule for division of fractions, "invert the divisor and multiply by the reciprocal". Though most of us solve basic problems like the above two without thinking that we are dividing fractions, we need to understand the connection to division of fractions so that we will be able to solve more complex problems.

Example:

You need to lay tile to create a frieze above a doorway. The tile measures 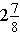inches by 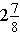inches. If the doorway is 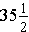inches wide, how many pieces of tile are needed? Write a mathematic expression for this problem. Solution   

return to top | next page