Fraction Division

Model for Division of Fractions

Remember the missing-factor definition for division:   a ÷ b = c if and only if b · c = a. With whole numbers this meant that 12 ÷ 3 = 4 precisely because 3 · 4 = 12. Also remember that division answers questions like "how many groups of 3 items can be made out of 12 items?" The division answer above tells us that when we have 12 items we can form 4 groups of 3 items each.

The same relationship defines division of fractions, e.g., 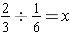if and only if 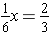. To see what happens, we solve this problem using a model first. This division problem answers the question "how many groups of 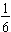  can be made out of ?"

So we begin with a whole divided into 3 equal pieces.

Since we start with 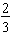, we need to shade 2 of the pieces to represent this amount.

Next we need to determine how many groups of 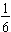can be formed from the shaded region. Notice that we can make the whole into six equal pieces in this picture,

Hence, the whole is in sixths. The shaded region contains 4 of these sixths. Therefore, because we can see that there are 4 of these sixths in the shaded .

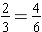return to top | previous page | next page