TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

       3.2.3 Affine Transformation of the Euclidean Plane  Printout
A mathematician, like a painter or a poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with ideas.
 —Godfrey Harold Hardy (1877–1947)

 

        What is the form of a transformation matrix for the analytic model of the Euclidean plane? We investigate this question. Let A = [a_ij] be a transformation matrix for the Euclidean plane and (x, y, 1) be any point in the Euclidean plane. Then

.

Since the last matrix must be the matrix of a point in the Euclidean plane, we must have a₃₁x + a₃₂y + a₃₃ = 1 for every point (x, y, 1) in the Euclidean plane. In particular, the point (0, 0, 1) must satisfy the equation. Hence, a₃₃ = 1. Further, the points (0, 1, 1) and (1, 0, 1) satisfy the equation and imply a₃₂ = 0 and a₃₁ = 0, respectively. Therefore, the transformation matrix must have the form

,

which motivates the following definition.

 

Definition. An affine transformation of the Euclidean plane, T, is a mapping that maps each point X of the Euclidean plane to a point T(X) of the Euclidean plane defined by T(X) = AX where det(A) is nonzero and

 where each a_ij is a real number.

 

Exercise 3.19. Prove that every affine transformation of the Euclidean plane has an inverse that is an affine transformation of the Euclidean plane. (Hint. Write the inverse by using the adjoint. Refer to a linear algebra text.)

Proposition 3.3. An affine transformation of the Euclidean plane is a transformation of the Euclidean plane.

 

Exercise 3.20. Prove Proposition 3.3.
 

Click here to see an animation of a sequence of affine transformations.
 

          

Proposition 3.4. The set of affine transformations of the Euclidean plane form a group under matrix multiplication.

 

Proof. Since the identity matrix is clearly a matrix of an affine transformation of the Euclidean plane and the product of matrices is associative, we need only show closure and that every transformation has an inverse.
      Let A and B be the matrices of affine transformations of the Euclidean plane. Since det(A) and det(B) are both nonzero, we have that det(AB) = det(A) · det(B) is not zero. Also,

 

is a matrix of an affine transformation of the Euclidean plane. (The last row of the matrix is 0 , 0, 1.) Hence closure holds.
      Complete the proof by showing the inverse property.//

 

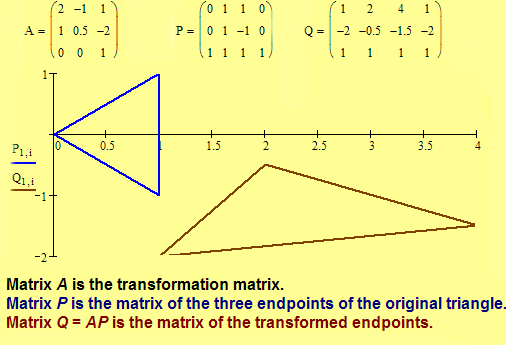
Exercise 3.21. Given three points P(0, 0, 1), Q(1, 0, 1), and R(2, 1, 1), and an affine transformation T. (a)  Find the points P' = T(P), Q' = T(Q), and R' = T(R) where the matrix of the transformation is .  (b)  Sketch triangle PQR and triangle P'Q'R' .  (c)  Describe how the transformation moved and changed the triangle PQR.

 

Exercise 3.22.  Find the matrix of an affine transformation that maps P(0, 0, 1) to P'(0, 2, 1), Q(1, 0, 1) to Q'(2, 1, 1), and R(2, 3, 1) to R'(7, 9, 1).

 

Exercise 3.23.  Show the group of affine transformations of the Euclidean plane is not commutative.