TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

3.5.2 Reflection of the Analytic Euclidean Plane Model  Printout
Nature often holds up a mirror so we can see more clearly the ongoing processes of growth, renewal, and transformation in our lives.
—Mary Ann Brussat

      The investigations from the last section indicate that a reflection of the Euclidean plane is an indirect isometry. What form does the matrix of an affine reflection of the Euclidean plane have? Let's investigate that question. To simplify the problem, we first consider the problem with the line h[0, 1, 0] (the x-axis) as the axis of reflection. Let X(x₁, x₂, 1) be an arbitrary point in the Euclidean plane with image X' under the reflection R_h.

 

Since every point on h is invariant and has the form X(x₁, 0 , 1), we must have x₁ = a₁₁x₁ + a₁₃ and 0 = a₂₁x₁ + a₂₃. Thus, since (0, 0, 1) is on h, a₁₃ = 0 and a₂₃ = 0. And, since (1, 0, 1) is on h, a₁₁ = 1 and a₂₁ = 0. Since R_h maps the point (0, 1, 1) to (0, –1, 1), a₁₂ = 0 and a₂₂ = –1. Hence,

 

We need to show that A is the matrix of the reflection R_h. Matrix A maps an arbitrary point X(x₁, x₂, 1) to the point X'(x₁, x₂, 1). If X is on h, then x₂ = 0 and X' is on h. If X is not on h, then the midpoint (x₁, 0, 1) of segment XX' is on h and the line through X and X' is l [1, 0, –x₁]. Since 0(1) + 1(0) = 0,  by the definition of the measure of an angle between two lines. Therefore, A is the matrix of the reflection R_h. Since det(A) = –1, the reflection R_h is an indirect isometry.

      What is the form of the matrix for a reflection R_l other than R_h? We can apply a method similar to the method used with a rotation that was not centered at the origin. If l is parallel to h, use a translation T that translates h to l and define . If l is not parallel to h, then l and h intersect at some point P, use a rotation  that translates h to l and define .
      We summarize our results above and from the previous section with the following proposition.

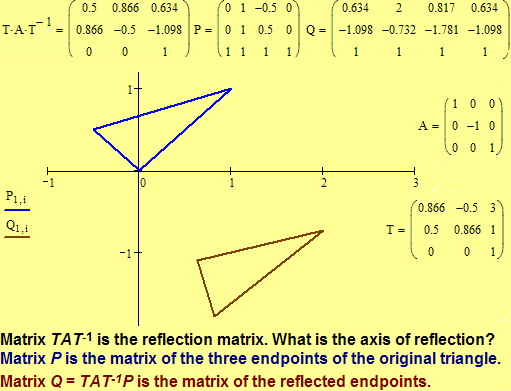
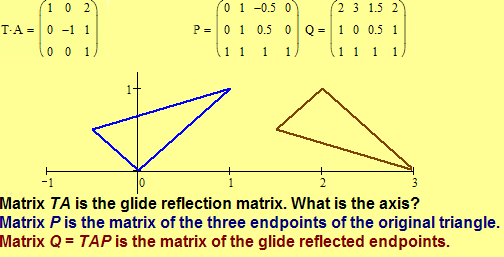
Proposition 3.15. (a) An affine reflection of the Euclidean plane is an indirect isometry. (b) Any affine indirect isometry of the Euclidean plane with exactly one line with all points invariant under the isometry is a reflection. (c) The matrix representation of an affine reflection of the Euclidean plane with axis h[0, 1, 0] is

 

(d) The matrix representation of an affine reflection of the Euclidean plane with axis l distinct from h is  where T is a direct isometry that maps line h to line l.

Exercise 3.80. Find a matrix of the reflection R_l where (a)  l[1, –1, 0]  (b) l[0, 1, –4], then for each reflection find the image of (4, 4, 1) and  

Exercise 3.81. Find a matrix of the reflection R_l where , and find the image of (2, 8, 1), (4, 4, 1), and (10, 7, 1).

Exercise 3.82. Find a matrix of the reflection that maps the point X(3, 8, 1) to Y(5, 1, 1) and find the image of Z(12, 7, 1).

Exercise 3.83. Find a matrix of the reflection that maps the line l[2, 3, –1] to m[2, 3, 5].

Exercise 3.84. Find a product of reflections that maps X(–2, 5, 1), Y(–2, 7, 1), and Z(–5, 5, 1) to X'(4, 3, 1), Y'(6, 3, 1), and Z'(4, 0, 1).

Exercise 3.85. Verify part (d) of Proposition 3.15.

3.5.1 Reflections and Glide Reflections 3.6.1 Similarity Transformations

© Copyright 2005, 2006 - Timothy Peil