TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

3.4.1 Translations and Rotations  Printout
By three methods we may learn wisdom: First, by reflection, which is noblest; Second, by imitation, which is easiest; and third by experience, which is bitterest.
—Confucius (551–479 B.C.)

 

Definition.  A translation through a vector PQ is a transformation of a plane, denoted T_PQ, such that if T_PQ maps X to X', then the vector XX' = PQ.

Definition.  A rotation about a point C through an angle with measure , denoted , is a transformation of a plane where C is mapped to itself and for any point X distinct from C if  maps X to X', then d(X', C) = d(X, C) and . C is called the center of the rotation.

By convention, the angle rotation is considered to be a counter-clockwise rotation. Also, angle measure is extended to any real number value by use of the Supplement Postulate and Angle Addition Postulate. As illustrated in the diagram, the 210° angle is formed from the sum of 30°, 150°, and 30° angles by use of vertical angles and the axioms. The reader should be able to justify the extension process from the axioms.

Definition. A transformation f is a symmetry of a point set if and only if the point set is invariant under the transformation.

Examples.  An infinite linear list of circles    …O O O O O O O…  has translation symmetry. What is a translation vector for this list? A square has four rotation symmetries: rotations of 0°, 90°, 180°, and 270° about the center of the square.

Investigation Exercises.  Is each transformation an isometry? If yes, is it a direct or indirect isometry?

3.46.  Draw a right triangle  with right angle at C. Accurately draw its image under each transformation.
     (a)  T_AC

     (b)  T_AM where M is the midpoint of .
     (c)  R_A,90

     (d)  R_C,150

 

3.47.  Draw the image of each transformation (a)  T_PQ  (b)  R_c,240 .

      
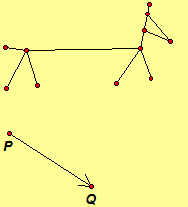
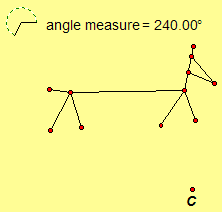
Click here to investigate dynamic illustrations of the above diagrams with GeoGebra html or JavaSketchpad.
                               

3.48.  Complete the table of the compositions of rotation symmetries for an equilateral triangle. An animation sketch is available for Geometers Sketchpad in Geometers Sketchpad and GeoGebra Prepared Sketches and Scripts.

	I = RO,0	RO,120	RO,240
I = RO,0
RO,120
RO,240

     Is the set of rotation symmetries of an equilateral triangle a group? Explain.

 

3.49.  Complete a table of the compositions of the rotation symmetries for a square. Is the set of rotation symmetries of a square a group? Explain.

Theorem 3.11. A translation of a Euclidean plane is an isometry.

 

Proof.  Let T_PQ be a translation of a Euclidean plane. Let X and Y be two distinct points in the plane and X' = T_PQ(X) and Y' = T_PQ(Y). By the definition of a translation,  are congruent and parallel. Two cases are possible: either X, X', Y, and Y' are not collinear or they are collinear.
      Assume X, X', Y, and Y' are not collinear. Since  are congruent and parallel, the quadrilateral XX'Y'Y is a parallelogram. Hence, XY = X'Y'.
      Assume X, X', Y, and Y' are collinear. Suppose the points are in the order X, Y, X', Y'. Then by betweenness of points and substitution, XY = XX' – YX' = YY' – X'Y = X'Y'. The subcases for other orders of the points are similar.
      In both cases XY = X'Y' for any two distinct points X and Y. Therefore, T_PQ is an isometry.//

 

Theorem 3.12. A nonidentity translation has no invariant points.

 

Theorem 3.13. The set of translations of a plane is a group under composition.

 

Theorem 3.14. There exists a unique translation mapping X to Y for any two distinct points X and Y in a Euclidean plane.

 

Theorem 3.15. Let P and Q be two distinct points in a Euclidean plane. Line  and all lines parallel to line  are invariant under the translation T_PQ. No other lines are invariant.

Proof.  Let P and Q be two distinct points in a Euclidean plane. By Theorem 3.14, there exists a unique translation T_PQ. First, we show the line PQ is invariant. Let X be a point on the line PQ. Then the line XX' is parallel to the line PQ where X' = T_PQ (X). If X' is not on line PQ, then the line XX' would intersect the line PQ at X, which contradicts that the lines XX' and PQ are parallel. Hence, X' is on line PQ. Therefore, line PQ is invariant under T_PQ.
       Let l be any line parallel to line PQ. Let X be any point on l and X' = T_PQ (X). By the definition of translation, lines XX'  and PQ are parallel. By the Euclidean Parallel Postulate, l and XX' are the same line. Since every point on line l maps to a point on line l, l is invariant under T_PQ.
      We need to show there are no other lines that are invariant under T_PQ. Suppose line l is invariant under T_PQ and is not parallel to line PQ. Then l and line PQ intersect at some point X. Hence, X is on two invariant lines l and PQ. Hence, the image point X' = T_PQ(X) is on both lines. Since the two lines are distinct, we must have X = X', i.e., X  is an invariant point under T_PQ. But this contradicts Theorem 3.12. Hence, no other lines are invariant under T_PQ.//

Exercise 3.50.  Verify other subcases in Case 2 of the proof of Theorem 3.11.

 

Exercise 3.51.  Prove Theorem 3.12.

 

Exercise 3.52.  Prove Theorem 3.13.

 

Exercise 3.53.  Prove Theorem 3.14.

 

Theorem 3.16. A rotation of a Euclidean plane is an isometry.

 

Proof. Let  be a rotation of a Euclidean plane where C is the center. Let X and Y be two distinct points in the plane and  and . Either the points C, X, and Y are collinear or noncollinear.
      Assume C, X, and Y are collinear. Suppose C = X. Then by definition of , XY = CY = CY' = XY'. The case for C = Y is similar. Suppose X is between C and Y. By the definition of , CX = CX' , CY = CY' and  Since C-X-Y and ,  and C-X'-Y'. Hence, by substitution and betweenness of points, XY = CY  CX = CY'  CX' = X'Y'. 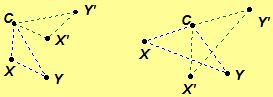The cases for other orders are similar.
      Assume C, X, and Y are noncollinear. Then by definition of , , , and  Similar to the argument using betweenness of points, we have by substitution and angle addition that  (Note that several cases must be considered; the details are left for Exercise 3.54.) Hence, by SAS,  Therefore, XY = X'Y'.
      In all of the cases, XY = X'Y' for any two distinct points X and Y; therefore,  is an isometry.//

 

Theorem 3.17. A nonidentity rotation has exactly one invariant point.

 

Theorem 3.18. The set of rotations with center C of a plane is a group under composition.

 

Exercise 3.54. (a) Verify the case where C is between X and Y in the proof of Theorem 3.16. (b) Verify the angle congruence for each case when the points were assumed to be noncollinear in the proof of Theorem 3.16.

 

Exercise 3.55.  Prove Theorem 3.17.

 

Exercise 3.56.  Prove Theorem 3.18.