Fraction Multiplication

Mixed Numbers Versus Improper Fractions

When we added mixed numbers, we found that it is usually easier to leave each addend as a mixed number and not change to improper fractions (see the previous session 21); whereas, when multiplying fractions it is usually easier to change to improper fractions and not leave as mixed numbers. We illustrate with the examples below. 

Example: Compute .

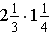We use the distributive property of multiplication over addition to compute the multiplication without changing the mixed numbers to improper fractions.

Now we rework the problem by first changing each mixed number into an improper fraction.

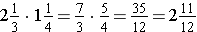
Note the fewer number of operations needed. Also, note that with the mixed number form we needed to find a common denominator to add the fractions. For some problems, the mixed number form is easier to use when making mental computations, but usually it is easier to work multiplication problems involving mixed numbers by changing to improper fractions. The opposite was true when adding and subtracting mixed numbers.

Example:  Evaluate .

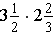Again, we use the distributive property of multiplication over addition to compute the multiplication without changing the mixed numbers to improper fractions.

Next, we rework the problem by first changing each mixed number into an improper fraction.

Summary:

1. It is usually easier to leave the terms as mixed numbers when adding or subtracting mixed numbers.
   
2. But, it is usually easier to change each mixed number to an improper fraction when multiplying mixed numbers.

 

 

return to top | previous page | next page