Fraction Division

Finding the Standard Algorithm for Dividing Fractions

 To illustrate, we consider the division problem 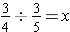. Instead of using a model this time, we solve this fraction division problem using the missing-factor definition of division, fraction multiplication, and properties for solving equations. This strategy will lead us to a general rule for computing division of fractions.

The following is an overview of the strategy we will use. A statement-reason table for this strategy appears later on this page. Read through this overview and then study the statement-reason table and try to follow the reasoning being used. In the end, we generate a simple rule for computing division of fractions, which is based on this strategy.

Overview

1. By the missing-factor definition of division, we know that 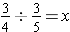if and only if .

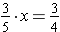2. Remember when we solved equations like 4x = 12 , we used a property of equality to divide both sides of the equation by 4 to get 1 · x = 3 or x = 3. We used a property of equality to get the x alone on the left side of the equation.

3. Using the same strategy on 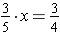, we need to find a value we can multiply both sides of the equation by so that that value times 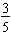equals 1. Since 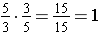, the value we need to multiply both sides of this equation by is .

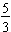4. Therefore, 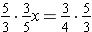and then 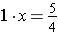and finally .

 

Statement-Reason Summary of Fraction Division Strategy

Statement Reason Summary of Fraction Division Strategy

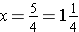Statement	Reason
	Original Problem
	Missing-Factor Definition of Division
	Multiplication Property of Equality  (Strategy: use so that )
	Associative Property of Multiplication
	Simplification of Fractions
	Inverse Property of Multiplication
	Identity Property of Multiplication

Note the above problem has 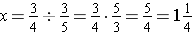, which follows the "invert the divisor and multiply by the reciprocal" rule.

In the previous example, we saw how the process of dividing fractions is based on rewriting the problem in its multiplication form and then solving by multiplying both sides of the equation by a value that will simplify the problem to the form 1 · x = ___ where ___ is a fraction multiplication problem. The key to this process is finding pairs of numbers that when multiplied equal one. In other words, we use the multiplicative inverse or reciprocal.

Self-Check Problem

You are going to bake cookies and only have three-fourths of a cup of flour. If the recipe states that two-thirds of a cup flour is needed to make a single batch of cookies. How many batches of cookies can you make if you use all of the flour? Solution

return to top | previous page | next page