Fraction Division

The Standard Algorithm for Dividing Fractions

Now we derive the general rule for dividing fractions.

Statement-Reason Table for Deriving the General Rule for Dividing Fractions

Statement	Reason
	Original Problem
	Missing-Factor Definition of Division
	Multiplication Property of Equality
	Associative Property of Multiplication
	Commutative Property of Multiplication
	Inverse Property of Multiplication
	Identity Property of Multiplication

Short-cutting all of the algebra steps shown in the previous table, we can generalize fraction division with the following formula.

Invert-and-Multiply Rule for Dividing Fractions

For a, b, c, and d, whole numbers with b, c, and d not equal to zero,

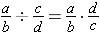
This may be described in words as "invert the divisor and multiply by the reciprocal." Some describe the rule as "change to divide and multiply by the reciprocal."

Example:

"Invert the divisor and multiply by the reciprocal" can seem like a strange and mysterious rule, but as we have seen, it follows from the definition of division, properties of multiplication, and properties of equality (definition, properties, and strategies for solving equations).

Self-Check Problem

You need to lay tile to create a frieze above a doorway. The tile measures 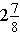inches by 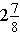inches. If the doorway is 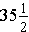inches wide, how many pieces of tile are needed?

Solution

Joke or Quote

Did you know that 5 out of every 4 people have a problem with fractions?

return to top | previous page