Decimal Fractions

Terminating Decimals and Repeating Decimals

Fractional Parts in the Place Value System

Earlier we learned about base-ten place value and how it is used to write whole number values. Now we extend the place-value concepts for the base-ten system to fractional parts of a whole.  

In that earlier lesson, we noticed how each column in the place value system represents a value ten times greater than the value of the column immediately to the right. Since that time, we have studied exponents and now see that these place values are consecutive "powers of 10".

If we continue the patterns of each column being ten times the value of the column to the right, the next column to the right would have to be a value that when it is multiplied by 10 would equal the value of the last column, which is 1. This means the value of the next column to the right must be tenths, since 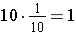. We abbreviate the common fraction 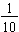  by writing the decimal fraction 0.1; both values are read as "one-tenth". We call the first place-value after the decimal point the tenths position. Notice that the decimal place values end in -ths. Tens are whole values and tenths are fractional parts of the whole.

If we extend to the right one more column, that value would have to be the value that when we multiply it by ten it would equal one-tenth. That means the next column to the right would be the hundredths, since 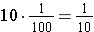. We abbreviate the common fraction 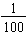as the decimal fraction 0.01. Again notice the "ths" ending. Hundreds are whole values and hundredths are fractional parts of the whole.

If we continue this process, we can extend the place value table out as far as we desire. As long as we have the table with the columns labeled, we can tell which column has which value. But when we write numbers without the table labels, we need to know where the place values change from whole numbers to fractions. That is the role of the decimal point. The decimal point separates the place values that are whole values on the left from the place values that are fractional parts on the right, as illustrated in the table below.

Note the thousandths position has a picture of the Missouri mill token; for more information on mill tokens used for taxes, see Mill (currency) - Wikipedia, the free encyclopedia.

return to top | previous page | next page