All common fractions can be written in decimal form. Some common fractions are easy to visualize as decimal fractions. For instance, we rewrite each of the common fractions, in the following examples, as a decimal by changing to an equivalent fraction that has denominator that is a power of ten. We use the fact that the prime factorization of each denominator has prime factors of 2 or 5, and the fact that the product of two and five is ten.
Examples: 
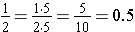or 
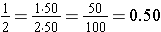
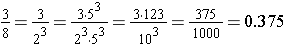
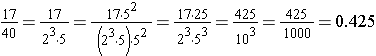
The above method works well when the denominator has only 2 or 5 as prime factors, but is there another method to convert common fractions? Another method to change a common fraction to a decimal fraction is to use the division interpretation of the fraction and continue the division on past the decimal point. In the example below, the division results in a terminating decimal
. That means that it divides out completely, eventually having a remainder of zero.
|
Examples: |
To show |
To show |
To show |
|
|
|
|
|
What about common fractions where the denominator has a prime factor other than 2 or 5?
Write 
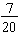as a decimal fraction.
return to top | previous page | next page
Content ©2010. All Rights Reserved.
Date last modified: June 24, 2010.
Created with SoftChalk LessonBuilder
By Kris Montis and Timothy Peil
