Comparing Decimals and Operations with Decimals

Decimal Order, Addtion, and Subtraction

Comparing and Ordering Decimals

When we compared and ordered fractions, we needed to find a common denominator. One of the advantages of using the decimal form of fractions is how much simpler it is to find common denominators.

Example: Compare 0.3 and 0.29.  

First, note that we are not comparing 3 and 29; we must consider the place-values of the 3 and 29. By use of place-value and writing 0.3 and 0.29 as common fractions, we see that we are comparing 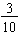and .

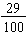But we can simplify this process by noting that these fractions have a common denominator simply by realizing 0.3 = 0.30. Extending decimal representations until they have the same number of decimal places automatically gives us common denominators.

So, to compare 0.30 to 0.29, we compare 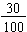and .

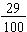Since , we conclude that 0.3 > 0.29.

The above example shows that we can compare terminating decimals by writing them with the same number of decimal positions; this is the same as finding a common denominator.

Example: Order the list 0.8, 0.123, 0.045, 0.03 from the least value to the greatest value.

We first rewrite the list as decimals with a common denominator, that is, we write each of the decimals in terms of thousandths: 0.800, 0.123, 0.045, 0.030. We now have

0.030 < 0.045 < 0.123 < 0.800.

By rewriting them in the original form, we conclude that

0.03 < 0.045 < 0.123 < 0.8.

If we are comparing both terminating and repeating decimals, we would want to write out enough repeating position to make the comparison clear.

Example: Order the list 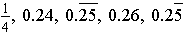from the least value to the greatest value.

We first rewrite each in decimal from with the same number of decimal positions:

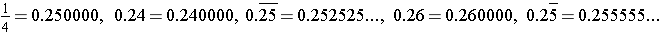
 We then have that 0.240000 < 0.250000 < 0.252525… < 0.255555… < 0.260000.

We conclude that .

Self-Check Problem

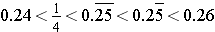A class of students at Hogwarts were comparing the lengths of their wands. Harry's wand was 2.4 decimeters long, Hermione's was 2.435 decimeters long, Ron's was 2.371 decimeters long, and Malfoy's was 2.39 decimeters long. Rank them from who had the longest to who had the shortest wand.

Solution

return to top | previous page | next page