Table of Contents

Motivation Problem

-------------------------

Review of Ratios

-------------------------

Solving Proportions with Equivalent Fractions

 

Brief Review of Ratios

See the previous Session 19 for an introduction to ratios.

Definition: A ratio is a comparison of the relative size of two numerical quantities. A ratio comparing quantity a to quantity b is usually written as a : b or in fraction form as 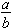and read verbally as the phrase "a to b."

Simplest Form: When writing a ratio, we will usually write it in simplest form. That is, we will simplify it so that the quantities involved have a greatest common factor of one.

Example: A garden is 20 feet long and 8 feet wide. Express the ratio of the length of the garden to the width of the garden in simplest form.

Ratio1.PNG

Order Matters: In a ratio, order is important. That is, the ratio a : b is not the same as the ratio b : a. A ratio compares two quantities in the order the items being quantified are listed.

Example: A small college has 35 faculty members and 1,000 students.  Express the student to faculty ratio in simplest form.  

Ratio2.PNG

The student to faculty ratio is 200 to 7, which is different than faculty to student ratio of 7 to 200. Since we were asked for the student to faculty ratio, the number of students must be listed in the numerator of the fraction form and as the first value in the colon notation.

A ratio gives us a nice way to compare the size of two quantities. If we are given two quantities, we can find the ratio of one to the other. Similarly, if we are given a ratio along with one of the original quantities, we can work backwards to find the second original quantity, as we did in the motivation problem with the chess club.

Example: Pat used three gallons of gas to drive seventy miles. If Pat used twelve gallons of gas, approximately how many miles could Pat drive?

The ratio of gallons of gas used to distance driven is 3 to 70. Since Pat used 12 gallons and 3(4) = 12, we could work the problem like we did with equivalent fractions. So, the ratio of 3 to 70 would be equivalent to the ratio of 3(4) to 70(4) or in other words 12 to 280. We conclude that Pat could drive 280 miles on 12 gallons of gas.

This problem leads to the concept of proportions, which is the equivalence of two ratios.

Self-Check Problem

 The full-time faculty to student ratio at MSUM is 1 to 23. If there are 325 full-time faculty members, approximately how many students are there?

Solution


return to top | previous page | next page