The Percent Equation

Solving Percentage Problems

Solving Percentage Problems

Reminder: A percent is a ratio that compares numerical quantities in terms of the number of parts out of 100.

In the previous session, we translated among the percent, decimal, and fractional forms of a value.   In this session, we take a percentage of a given quantity and solve problems involving percents.

The basic approach we use is to translate the problem into an equation and then solve the equation. It is often helpful to first restate the problem into an abbreviated form before translating the problem to an equation form. Key words are often helpful in the restatement and translation steps. For many of these percentage problems the verb "is" translates as "equals" and the preposition "of" translates as the operation of multiplication, "times".  

An example of translating a percent problem and then solving it would be:

Example: Dexter (the Kaputian monkey) steals the keys from Larry the watchman at the Museum of Natural History 46% of the nights. In the last 50 nights, how many nights has Dexter stolen the keys?

First clue: The missing number is the number of nights that Dexter has stolen the keys. We assign a variable to this missing value: Let x represent the number of nights Dexter stole the keys.

Restate: 46% of the last 50 nights is the number of times Dexter has stolen the keys.

Translate: 0.46 (50) = x   Note 46% = 0.46, of is times, is is equals, and x is the number of nights the keys were stolen.

Solve: x = 0.46(50) = 23

Answer: Dexter has stolen the keys 23 nights out of the last 50 nights.

Check: Does this sentence make sense in terms of the original problem?

Yes, we would expect the number of nights he stole the keys should be less than 50. Also, the ratio 23 to 50 is equivalent to the ratio 46 to 100 (or 46%).

Example: The figures from the diorama room are only 7.5% of the height of the people they represent. Approximately, how tall was Octavius if his diorama figure is only 5 inches tall? Augustus - Wikipedia, the free encyclopedia

First clue: The missing number is the height of the real Octavius. Let x represent the height of the real Octavius (in inches).

Restate: The 5-inch tall diorama figure is 7.5% of the height of the real Octavius.

Translate: 5 = 0.07(x)   Note is is equals , 7.5% = 0.075, of is times, and x is the height of the real Octavius.

Solve:  Since we need to solve this equation, we use our properties of equality as we have before.

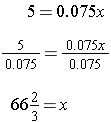
Answer: The original Octavius was 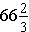inches tall, which is approximately 5 feet 7 inches.

The problem many people have with this technique is being able to restate the problem clearly as a percent relationship. We further explain the three basic parts of a percent relationship in the rest of the lesson.

Self Check Problem

You correctly answered questions worth sixty-eight points on a test that was 80% of the total points possible. How many total points were possible?

Solution

return to top | previous page | next page