Means, Frequency Tables, and Weighted Average

Mean from a Frequency Table

For large data sets in which values repeat often, the data is usually reported in a frequency table.   A frequency table summarizes a data set by showing how often each value occurs.

Example: Consider the following frequency table.

Data Value	10	20	30	40	50	60	70	80	90	100	110	120
Frequency	3	5	6	8	10	12	15	10	10	12	5	4

This table tells us that the data value 10 occurs 3 times in the data set, the data value 20 occurs 5 times in this data set, the data value of 30 occurs 6 times, etc.  The most frequent data value is 70, which occurred 15 times.

The sum of the frequencies is 100 since 3 + 5 + 6 + 8 + … + 4 = 100, which is the total number of data values. If we compute the mean the usual way, we would have to add up all 100 separate values and then divide by 100, since there are 100 data values reported.

A quicker method is to consider the frequencies as weights for each value. So in our table, the data value 10 has a weight of 3, because it occurred 3 times, while the data value 70 has a weight of 15 because it occurred 15 times.

For example, since 10 had a frequency of 3, we can multiply 10(3) = 30. This gives us the same total as if we had added the tens separately: 10 + 10 + 10 = 30. For data values like 70 which have a larger number of frequencies, this save us a lot of time since 15(70) is more efficient to compute than adding fifteen 70's.

By extending the frequency table to include the weighted values and the totals, we compute the mean using only the table, instead of having to write out and add all 100 separate values. Notice that the sum of all of the frequencies tells us how many separate values we have.

Data Value	10	20	30	40	50	60	70	80	90	100	110	120	Totals
Frequency	3	5	6	8	10	12	15	10	10	12	5	4	100
Weighted Value	30	100	180	320	500	720	1050	800	900	1200	550	480	6,830

The mean for this data set is .

Self Check Problem

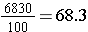The results from a twenty question placement exam for incoming students are summarized in the following frequency table. Find the mean score on the placement exam.

Score	9	11	12	13	14	15	16	17	18	19	20
Frequency	1	5	3	9	3	13	10	8	4	1	3

Solution

return to top | previous page | next page