Means, Frequency Tables, and Weighted Average

Weighted Average

A weighted average (weighted mean or scaled average) is used when we consider some data values to be more important than other values and so we want them to contribute more to the final "average". This often occurs in the way some professors or teachers choose to assign grades in their courses. For instance, a professor may want the exam grades to "weigh" more than quiz and homework grades when computing the final grade in the course.  

Example: Tully scored 70% on his midterm, 40% on his final exam, and had an average of 98% on his daily work (homework and quizzes). He believes his grade in the course will be 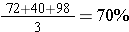. However, the course syllabus states that the midterm exam counts 40%, the final counts 50%, and all the daily work counts 10% of the final grade. What is Tully's actual grade in the course?

Solution: We need to find the grade which is composed of 40% of Tully's score on his midterm, 50% of Tully's grade on his final, and 10% of Tully's grade on his daily work.

We can make a table to help organize our computations.

	Midterm	Final Exam	Daily Grades	Total
Component Grade	70%	40%	98%	XXX
Component Weight	40%	50%	10%	100%
Weighted Value of Component Grades	0.40(70%) = 28%	0.50(40%) = 20%	0.10(98%) = 9.8%	57.8 points of 100 or 57.8%

Tully's semester grade is the sum of these weighted values:  

28% + 20% + 9.8% = 57.8%.

This is a lower grade than Tully was expecting because his highest grade (daily) had the least weight (10%) while his lowest grade (final exam) had a much higher weight (50%).

Self Check Problem

 Dr. Peil uses the following weighted mean to determine final grades for MDEV 102.

20% - Final Exam
50% - Five Unit Exams
10% - Collected Labs
10% - Collected Homework
10% - Supplemental Homework

Suppose Dana's grades were 74% on the final exam, 78% on the unit exams, 96% on the collected labs, 92% on the collected homework, and 94% on the supplemental homework. Determine Dana's final grade.

Solution

Joke or Quote

There are three different types of stock market brokers and advisors.

Those who don't know anything about stocks: approx. 10%

Those who know a little about stocks: approx. 10%

Those who don't realize they don't know anything about stocks but think they do: approx. 80%

return to top | previous page