Five-Number Summary and Box-and-Whisker Plots

Brief Review of Median

In previous sessions, we worked problems involving the mean and median. For this session, we primarily use the median. Here is a brief review of terms used with the median: 

• A data set is any finite set of real numbers.  
• A data set is in increasing order if the numbers in the data set are arranged from the least value to greatest value with the least value on the left and the greatest value on the right.
• The median of a data set is the number that, when the set is put into increasing order, divides the data into two equal parts.  
• If a data set has an odd number of data points, then the median is the middle data value (when the data is in increasing order).
• If a data set has an even number of data points, then the median is the mean of the two middle data values (when the data is in increasing order).

Example 1: Find the median of the data set {3, 7, 8, 5, 12, 14, 21, 13, 18}.

First, we put the values in the data set into increasing order: 3, 5, 7, 8, 12, 13, 14, 18, 21. Notice that the number of data values is 9, which is odd (there are nine numbers in this data set). Then the middle data value is the 5^th value, counting from either the left or the right. Therefore the median is 12.
(The values 3, 5, 7, and 8 are to the left of 12, and 13, 14, 18, and 21 are to the right of 12.)

 Example 2: Find the median of the data set {3, 7, 8, 5, 12, 14, 21, 15, 18, 14}.

Note that here we consider the two 14's to be distinct elements and not representing the same item; consider this like you obtained a score of 14 on two different quizzes.
First, we put the values into increasing order: 3, 5, 7, 8, 12, 14, 14, 15, 18, 21. Notice that there are 10 values, which is even. Then the middle data values are the 5^th value from the left and the 5^th value from the right. That is, 12 and 14 (the leftmost of the two 14s). Therefore the median is the mean of the two middle values: The median is . 

Self Check Problem

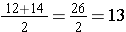The following dollar amounts were the hourly collections from a Salvation Army kettle at a local store one day in December: $19, $26, $25, $37, $32, $28, $22, $23, $29, $34, $39, and $31. Determine the median amount collected.

Solution

return to top | previous page | next page