Five-Number Summary and Box-and-Whisker Plots

First Quartile and Third Quartile

Definitions:

• The lower half of a data set is the set of all values that are to the left of the median value when the data has been put into increasing order.
• The upper half of a data set is the set of all values that are to the right of the median value when the data has been put into increasing order.
• The first quartile, denoted by Q₁ , is the median of the lower half of the data set. This means that about 25% of the numbers in the data set lie below Q₁ and about 75% lie above Q₁ .
• The third quartile, denoted by Q₃ , is the median of the upper half of the data set. This means that about 75% of the numbers in the data set lie below Q₃ and about 25% lie above Q₃ .

Example 1: Find the first and third quartiles of the data set {3, 7, 8, 5, 12, 14, 21, 13, 18}.

First, we write data in increasing order: 3, 5, 7, 8, 12, 13, 14, 18, 21.

As on the previous page, the median is 12.

Therefore, the lower half of the data is: {3, 5, 7, 8}.

The first quartile, Q₁, is the median of {3, 5, 7, 8}.

Since there is an even number of values, we need the mean of the middle two values to find the first quartile:

.

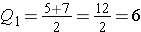Similarly, the upper half of the data is: {13, 14, 18, 21}, so

.

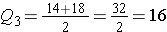Example 2: Find the first and third quartiles of the set {3, 7, 8, 5, 12, 14, 21, 15, 18, 14}.

Note that here we consider the two 14's to be distinct elements and not representing the same item; consider this like you obtained a score of 14 on two different quizzes.

First, we write the data in increasing order: 3, 5, 7, 8, 12, 14, 14, 15, 18, 21.

As before, the median is 13 (it is the mean of 12 and 14 — the pair of middle entries).

Therefore, the lower half of the data is: {3, 5, 7, 8, 12}.  

Notice that 12 is included in the lower half since it is below the median value.

Then Q₁ = 7 (there are five values in the lower half, so the middle value is the median). Similarly, the upper half of the data is: {14, 14, 15, 18, 21}, so Q₃ = 15.

Self Check Problem

The following dollar amounts were the hourly collections from a Salvation Army kettle at a local store one day in December: $19, $26, $25, $37, $32, $28, $22, $23, $29, $34, $39, and $31. Determine the first quartile and third quartile for the amount collected.

Solution

return to top | previous page | next page