1.2 A Finite Geometry  Printout
As a basis for our study we assume an arbitrary collection of entities of an arbitrary nature, entities which for brevity, we shall call points, and this quite independently of their nature.
—Gino Fano (1871–1952)

        Gino Fano (1871–1952) is credited with being the first person to explore finite geometries beginning in 1892. He worked primarily in projective and algebraic geometry. He was born in 1871 in Mantua, Italy. He initially studied in Turin. Later, he moved to Göttingen and worked with Felix Klein. Fano served as a professor of mathematics in Turin until he was forced to leave during World War II. He also taught in Switzerland and the United States. He died in Verona, Italy in 1952.

        Fano initially considered a finite three-dimensional geometry consisting of 15 points, 35 lines, and 15 planes. Here, we obtain a finite geometry by restricting the system to one of the planes.

Axioms for Fano's Geometry

Undefined Terms. point, line, and incident.
Axiom 1. There exists at least one line.
Axiom 2. Every line has exactly three points incident to it.
Axiom 3. Not all points are incident to the same line.
Axiom 4. There is exactly one line incident with any two distinct points.
Axiom 5. There is at least one point incident with any two distinct lines.

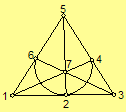        Here are two isomorphic models for Fano's Geometry:
In the diagram model on the left, points are defined by the seven dots and lines by the six straight segments and one curved segment. Note each line contains exactly three points.

The second model is illustrated in the table below.

Exercise 1.4. Verify the models satisfy the axioms. (Since checking every case for Axioms 4 and 5 would be tedious, check enough cases to show sufficient understanding.) For Axioms 4 and 5, how many cases need to be checked to verify each model?

Exercise 1.5. Show the two models for Fano's geometry are isomorphic.

Exercise 1.6. Show each of the axioms for Fano's geometry is independent.

Fano's Theorem 1. Two distinct lines intersect in exactly one point.

Proof. Let p and q be any two distinct lines. By Axiom 5, there is a point A incident to both p and q. Suppose there is a second point B, distinct from A, incident to both p and q. Then by Axiom 4, p and q are the same line, but this contradicts that p and q are distinct lines. Thus p and q intersect in exactly one point A. Therefore, two distinct lines intersect in exactly one point.//

Fano's Theorem 2. Fano's geometry consists of exactly seven points.

Proof. By Axiom 1, there exists a line l. Then by Axiom 2, there exist exactly three points A, B, C on line l. Now by Axiom 3, there exists a point P not on line l. Hence we have at least four distinct points A, B, C, and P. By Axiom 4 and since P is not on line l, there are three distinct lines AP, BP, and CP. And by Axiom 2, each of these lines contains a third point D, E, and F on AP, BP, and CP, respectively. None of D, E or F can be any of the points A, B, C, or P; for if this was not true, Axiom 4 would be contradicted. (Write the details for this argument in Exercise 1.7.) Hence there are at least seven distinct points A, B, C, D, E, F, and P.
        We assert that there are exactly seven distinct points. Suppose there exists a distinct eighth point Q. Note Q is not on l, since A, B, and C are the only points on l. By Axioms 4 and 5, lines PQ and l must intersect at a point R. Since A, B, and C are the only points on l, R must be one of A, B, or C. Suppose R = A. Since D is on line AP and A = R is on line PQ, we would have R = A, D, P, and Q collinear which contradicts Axiom 2. The other cases for B or C are similar. Hence there are exactly seven distinct points.//

Exercise 1.7. Write the contradiction argument within the proof of Fano's Theorem 2 to show that A, B, C, D, E, F, and P are distinct points.

Fano's Theorem 3. Each point in Fano's geometry is incident with exactly three lines.

Fano's Theorem 4. Fano's geometry consists of exactly seven lines.

Exercise 1.8. Prove Fano's Theorem 3.

Exercise 1.9. Prove Fano's Theorem 4.

Exercise 1.10.  Write the dual for Fano's axioms. Does Fano's geometry satisfy the principle of duality? (Briefly justify.)

Exercise 1.11.  A four-point geometry.

Undefined terms. point, line, and on
Axiom 1. There exist exactly four points.
Axiom 2. Two distinct points are on exactly one line.
Axiom 3. Each line is on exactly two points.

1. Show this axiomatic system is consistent.
2. Is the system complete? Explain.
3. Show the axioms are independent.
4. Prove the following theorems.
       T1. If two distinct lines intersect, they intersect in exactly one point.
       T2. A four-point geometry has exactly six lines.
       T3. Each point has exactly three lines on it.
       T4. Each distinct line has exactly one line parallel to it.
5. Show any two models are isomorphic.
6. Write the dual of the four-point geometry creating a four-line geometry.
7. Compare the four-point geometry to Exercise 1.2 of Examples of Axiomatic Systems.

Contradiction is not a sign of falsity, nor the lack of contradiction a sign of truth.
—Blaise Pascal (1623–1662)