TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

               2.1.3 Analytic Models for Plane Geometry  Printout
The ludicrous state of solid geometry made me pass over this branch.
—Plato Republic (429–347 B.C.)

 

      This section lists analytic models that will be used in the study of plane geometry. The models are to help to better understand the axioms for neutral geometry (Euclidean geometry and hyperbolic geometry). As we progress through the SMSG axiom set, a model will be dropped when it no longer satisfies the axioms in use.

 

Definition. A distance function on a set S  is a function  such that for all  

i.        d(A,B)  0;

ii.      d(A,B) = 0 if and only if A = B;

iii.    d(A,B) = d (B,A).

Here, we do not list the Triangle Inequality as part of the definition of a distance function, since other axioms will give us the Triangle Inequality as a theorem.

Discrete Planes. Let S be a nonempty set. The points are the elements of S. The lines are a specified collection of nonempty subsets of S. The distance function  is defined by

.

Riemann Sphere. The points are elements of the unit sphere . The lines are great circles, G, of the unit sphere S² formed by the intersection of S²  and a plane through the origin; that is, there are  not all zero such that G = {(x, y, z) ϵ S² : ax + by + cz = 0}.   Click here for a java exploration of the Riemann Sphere model.

Modified Riemann 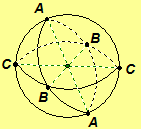Sphere. The points, {(x, y, z), (–x, –y, –z)}, are polar pairs (antipodal points) on the unit sphere . The lines are the modification of the great circles of the Riemann Sphere. In the illustration of a sphere on the right, the Modified Riemann Sphere has three points A, B, and C. Each polar pair of points (antipodal points) is considered to be a single point. Also, three lines are shown, line AB, line AC, and line BC, which consist of the great circles passing through the polar point pairs. The segments connecting the polar points and the center of the sphere are not in the plane determined by the Modified Riemann Sphere; they are only drawn to help with visualization of the polar pairs. In some sense, the Modified Riemann Sphere may be thought of as a hemisphere with half of the equator.

 

Cartesian Plane. A point is an ordered pair (x, y) where , i.e.  is the set of all points.  The lines are either vertical l_a = {(x, y) : x = a} or  nonvertical l_m,b = {(x, y) : y = mx + b}. Note that these are the definitions for points and lines used in high school algebra.

 

Euclidean Plane. The points and lines for the Euclidean plane are the Cartesian points and lines with the addition of a distance function  defined by

 

The standard ruler, , for a nonvertical line is defined by
The standard ruler, , for a vertical line is defined by f(a, y) = y.
The angle measure of  is defined by  where  is the dot product (inner product) of the two vectors and  is the magnitude of the vector. Note the definition for angle measure is motivated from results in vector calculus or linear algebra. Check your textbooks from those two courses.

 

Geometer's Sketchpad sketch with tools to explore ruler's in the Euclidean, Taxicab, and Max-Distance planes is available in Appendix B of the Course Title Page - Prepared Geometer's Sketchpad and GeoGebra Sketches.

Taxicab Plane. The points and lines for the Taxicab plane are the Cartesian points and lines with the addition of a distance function  defined by

.

The standard ruler, , for a nonvertical line is defined by f(x, y) = (1 + |m|)x.
The standard ruler, , for a vertical line is defined by f(a, y) = y.

Max-Distance Plane. The points and lines for the Max-distance plane are the Cartesian points and lines with the addition of a distance function  defined by

.

The standard ruler, , for a nonvertical line is defined by .
The standard ruler, , for a vertical line is defined by f(a, y) = y.

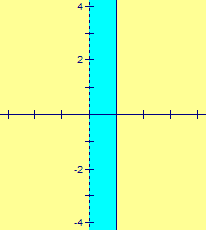
Missing Strip Plane. A point is an element of the set . The lines are modified Cartesian lines; a line is defined by a Cartesian line intersected with set M (explore Missing Strip lines GeoGebra html5 or JavaSketchpad), i.e. the lines are elements of the set . The distance function   for two points on a vertical line is defined by the Euclidean distance between the two points. The distance function for two points on a nonvertical line is defined by  where  and g_l  is defined from the standard ruler f_l of the Euclidean plane by

 

where m is the slope of line l. Note the Missing Strip plane is simply the Euclidean plane with a vertical strip removed and all the necessary adjustments so that no distance is measured across the missing region. In the diagram on the right, the light blue region (river through a town) is not part of the plane.
      A prepared Geometer's Sketchpad sketch and GeoGebra sketch with tools for constructions in the Missing Strip plane are available in Appendix B of the Course Title Page - Prepared Geometer's Sketchpad and GeoGebra Sketches.

 

Poincaré Half-Plane. The points are the elements of the set , i.e. the upper half-plane of the Cartesian plane. The lines are of two types: vertical rays which are any subset of H of the form , called Type I lines; or semicircles which are any subset of H of the form , called Type II lines (explore Poincaré lines GeoGebra html5 or JaveSketchpad). The distance function  is defined by

.

The standard ruler, , for a Type I line is defined by f(a, y) = ln y.
The standard ruler, , for a Type II line is defined by .
Angle measure for  is defined by  where for the ray BA the vector T_BA is defined by

 

      Click for a GeoGebra html5 or javasketchpad illustration of lines in the Poincaré Half-plane.
      Click for a GeoGebra html5 or javasketchpad illustration of lines in the Missing Strip plane.
      Click for a GeoGebra html5 or javasketchpad illustration of angle measure in the Poincaré Half-plane.
      A prepared Geometer's Sketchpad sketch and GeoGebra sketch with tools for constructions in the Poincaré Half-plane is available in Appendix B of the Course Title Page - Prepared Geometer's Sketchpad and GeoGebra Sketches. Also, an on-line java based program called NonEuclid may be used for constructions in the Poincaré Half-plane at http://cs.unm.edu/~joel/NonEuclid.
      Another model used for hyperbolic geometry is the Poincaré Disk. A prepared sketch for the Poincaré Disk comes with Geometer's Sketchpad. It is located in the Geometer's Sketchpad program folder: Samples  Sketches  Investigations. Also, NonEuclid contains the Poincaré Disk model.

 

Proposition 2.1. The Euclidean distance function is a distance function.

Proof. Let (x₁, y₁) and (x₂, y₂)  be points in the Euclidean plane. We need to show the d_E satisfies the three conditions defining a distance function.
Condition (1). We have  and . Hence, . Thus condition (1) is satisfied.
Condition (2).  d_E((x₁, y₁), (x₂, y₂)) = 0 iff  iff  (x₂ – x₁)² + (y₂ – y₁)²  = 0 iff (x₂ – x₁)²  = 0  and (y₂ – y₁)²  = 0  iff x₂ – x₁ = 0 and y₂ – y₁ = 0 iff x₂ = x₁  and y₂ = y₁ iff (x₁, y₁) = (x₂, y₂). Thus condition (2) is satisfied.
Condition (3).

 

Thus condition (3) is satisfied.
      Hence the Euclidean distance function is a distance function. //

 

Exercise 2.3. For each model (Euclidean, Taxicab, Max-distance, Missing-Strip, and Poincaré Half-plane), find the distance between points P(–1, 2) and Q(3, 4).

 

Exercise 2.4. Show the Taxicab distance satisfies the definition of distance.

 

Exercise 2.5. Show the Max-distance distance satisfies the definition of distance.

 

Exercise 2.6. Show the Missing Strip distance satisfies the definition of distance.

 

Exercise 2.7. Show the Poincaré Half-plane distance satisfies the definition of distance.

 

Exercise 2.8. (a) Show the Hamming distance satisfies the definition of distance. (b) Does the Discrete Plane distance satisfy the definition of distance? Justify.

 

Exercise 2.9. Define a distance function for the Modified Riemann Sphere.

 

Exercise 2.10. Sketch and describe a circle for each model.