1.4 Applications of Finite Geometry
![]() Printout
Printout
One of the characteristics of successful
scientists is having courage. Once you get your courage up and believe that you
can do important problems, then you can. If you think you can't, almost surely
you are not going to.
—![]() Richard W. Hamming
(1915–1998)
Richard W. Hamming
(1915–1998)
If you don't work on important problems, it's
not likely that you'll do important work.
—![]() Richard W.
Hamming
(1915–1998)
Richard W.
Hamming
(1915–1998)
The advances in computer technology have led to the need for good error-correcting codes. Information is sent, received, and processed in a digital format from transmission of data between computers and cell phones to the reading of data in shipping and price scanning. The problem is how to correct or minimize the errors that occur in the sending, receiving, and scanning of data. Research in coding theory uses results from projective geometry, group theory, and linear programming.
![]() Richard W. Hamming (1915–1998) was the
first person to devise error-correcting codes while he worked for Bell
Telephone laboratories in the 1940’s. The motivation for devising
error-correcting codes arose from Hamming’s frustration with often needing to
restart computations. Errors in data entry occurred often when the punch cards,
which were used to store and enter data, were read. In 1950, he published his
results that are now referred to as the
Richard W. Hamming (1915–1998) was the
first person to devise error-correcting codes while he worked for Bell
Telephone laboratories in the 1940’s. The motivation for devising
error-correcting codes arose from Hamming’s frustration with often needing to
restart computations. Errors in data entry occurred often when the punch cards,
which were used to store and enter data, were read. In 1950, he published his
results that are now referred to as the
![]() Hamming Code. One of the algorithms,
the
Hamming Code. One of the algorithms,
the
![]() Hamming (7, 4) code, can detect and correct single-bit errors. Some
applications still use codes developed by Hamming. The Hamming (7, 4) code is
not the best choice due to the non-standard character length of 7-bits and its
limitation to finding and correcting errors in a single bit position. Though
Hamming did not develop the Hamming (7, 4) code in the manner described in this
section, it is a nice example for illustrating relationships finite geometries
have to real applications.
Hamming (7, 4) code, can detect and correct single-bit errors. Some
applications still use codes developed by Hamming. The Hamming (7, 4) code is
not the best choice due to the non-standard character length of 7-bits and its
limitation to finding and correcting errors in a single bit position. Though
Hamming did not develop the Hamming (7, 4) code in the manner described in this
section, it is a nice example for illustrating relationships finite geometries
have to real applications.
The ‘7’ in the Hamming (7, 4) code represents the number of bits used to represent a codeword written as a binary numeral, e.g., 1001100. The ‘4’ is for the first four bit positions which are the information data bits, that is, the first four bits give the binary representation of the sixteen decimal numbers 0 through 15 (0000, 0001, 0010, …, 1111) that represent the word or message. Note that the binary numeral 1101 is 13 as a decimal numeral since 1(23) + 1(22) + 0(21) + 1(20) = 13. The last three bit positions are the redundant data bits used to check for errors. Note that these three positions are the binary version of the seven nonzero decimal numerals 1 through 7. From these, define the parity matrix
.
Now use a basis for the kernel of matrix Hp to form the generator matrix
where computations are modulo 2. Since the first four rows of He form the identity matrix, we encode a word by multiplying modulo 2. For example, the word 1101 becomes the codeword 1101001,
.
The codeword for each of the sixteen possible words are listed in the table below.
|
Codeword Table |
||||||
| 0000000 | 1111111 | 0001111 | 1110000 | |||
| 1000011 | 0111100 | 1100110 | 0011001 | |||
| 0100101 | 1011010 | 1010101 | 0101010 | |||
| 0010110 | 1101001 | 1001100 | 0110011 | |||
Note that each codeword in the second and fourth columns is the binary complement of the codeword in the first column and third columns, respectively. You should verify that each codeword is in the kernel of the parity matrix Hp. Also, the columns of He written as vectors (code words) form a basis for the set of vectors (code words) in the Codeword Table, that is, the code words in the Codeword Table are the elements of the kernel of matrix Hp.
How do the code words relate to a finite geometry? Consider a matrix model for Fano’s Geometry where points are the columns and lines are rows where a ‘1’ indicates a point is incident with a line and a ‘0’ indicates a point is not incident with a line.
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | |
| l1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| l2 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| l3 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| l4 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| l5 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| l6 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| l7 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
Each of these seven lines is a codeword in the Codeword Table. Also, these seven lines as vectors (code words) span the kernel of matrix Hp, i.e., they span the set the code words in the Codeword Table.
How does the algorithm for the Hamming code identify an error in the transmission of a codeword? An assumption is made that there is at most one bit error in the transmission of the codeword. Suppose the codeword 1101110 is received.
Since the vector (1, 0, 0) is not the zero vector, the codeword is not in the kernel of Hp. Hence a transmission error occurred. The binary numeral 100 represents the decimal number 4 since 1(4) + 0(2) + 0(1) = 4. Thus the error occurs in the fourth position. Assuming a single bit error, the codeword should be 1100110.
We use a finite geometry to justify why the Hamming (7, 4) code should always work for transmitting a seven bit codeword with the assumption of at most a single bit error. Consider the seven-dimensional finite space consisting of all possible binary 7-tuples, i.e., each seven bit codeword is point in the model of the finite geometry. The space consists of 27 points (128 code words). Only sixteen of these 128 points are considered to be code words with no transmission errors. Hamming considered a distance function to measure, in some sense, how far the points are apart.
Definition. The Hamming distance between any two binary n-tuples x and y is
,
i.e., the number of components by which the n-tuples
differ.
 For
example, d(1100101, 1010110) = 4 since the two 7-tuples differ in the
second, third, sixth, and seventh positions. In the seven-dimensional space, the
minimum Hamming distance between points listed in the Codeword Table is three
and the maximum distance between any two code words is seven. Also, each
codeword has exactly seven other code words at a Hamming distance of one. Thus,
we consider each point (codeword) to be the center of a sphere of radius one
that consists of exactly seven distinct points. The sixteen points (code words),
listed in the Codeword Table, determine sixteen distinct spheres of radius one
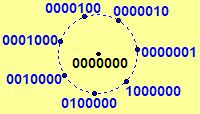
of which no two of the spheres intersect. (See the diagram on the left.) These sixteen spheres account for all
the 128 points in the seven-dimensional finite space (verify). This result applied to the Hamming (7, 4) codeword
implies that a transmitted codeword with an error in a single bit must be a Hamming distance of one from a
valid codeword. The algorithm makes the correction by changing the single
incorrect bit position.
For
example, d(1100101, 1010110) = 4 since the two 7-tuples differ in the
second, third, sixth, and seventh positions. In the seven-dimensional space, the
minimum Hamming distance between points listed in the Codeword Table is three
and the maximum distance between any two code words is seven. Also, each
codeword has exactly seven other code words at a Hamming distance of one. Thus,
we consider each point (codeword) to be the center of a sphere of radius one
that consists of exactly seven distinct points. The sixteen points (code words),
listed in the Codeword Table, determine sixteen distinct spheres of radius one
of which no two of the spheres intersect. (See the diagram on the left.) These sixteen spheres account for all
the 128 points in the seven-dimensional finite space (verify). This result applied to the Hamming (7, 4) codeword
implies that a transmitted codeword with an error in a single bit must be a Hamming distance of one from a
valid codeword. The algorithm makes the correction by changing the single
incorrect bit position.
A matrix model for Fano’s Geometry produces a spanning set for the valid code words in the Hamming (7, 4) Code. As noted in Section 1.3, Fano’s Geometry is a projective geometry of order 2. Projective geometries of other orders can be used to develop other error-correcting codes.
Exercise 1.22. Show the columns of matrix He determine a basis for the kernel for matrix Hp. Note all computations are modulo 2.
Exercise 1.23. Verify that the matrix He encodes the sixteen binary numerals 0000, 0001, …, 1111 as given in the Codeword Table. Note all computations are modulo 2.
Exercise 1.24. Show the matrix model for Fano’s Geometry is isomorphic to the two models given in Section 1.2.
Exercise 1.25. Show the lines in the matrix model for Fano’s Geometry as vectors (code words) span the kernel of matrix Hp.
Exercise 1.26. Use the generator matrix to encode the words 1011, 0101, and 1001. Note all computations are modulo 2.
Exercise 1.27. Assume each codeword has at most a single bit error. Use the parity matrix to identify the position of the error for 1011100, 0101001, and 1001101. Note all computations are modulo 2.
Exercise 1.28. Verify that the Hamming distance between each pair of code words in the Codeword Table is at least three.
Mathematics is an interesting intellectual
sport but it should not be allowed to stand in the way of obtaining sensible
information about physical processes.
—![]() Richard W. Hamming (1915–1998)
Richard W. Hamming (1915–1998)
|
© Copyright 2005, 2006 - Timothy Peil |