2.6.1 Parallel Lines without a Parallel
Postulate
![]() Printout
Printout
Mathematics consists of proving the most
obvious thing in the least obvious way.
—![]() George Polyá (1887–1985)
George Polyá (1887–1985)
Before adding a
parallel postulate to our study, we consider several questions about parallel
lines. Do parallel lines exist? How can we prove two lines are parallel? What
do we know about parallel lines without a parallel postulate?
Definitions.
Two lines are
parallel if and only if they do not
intersect.
Given , if A-C-D,
then
is an exterior angle of
Also,
and
are called remote interior angles.
Given line AB, line DE, and line BE such that A-B-C, D-E-F, and G-B-E-H where
A and D on the same side of line BE, then line BE is called a transversal.
Angles and
(also
and
) are called alternate interior angles.
![]() The next theorem will be useful in
proving two lines are parallel. From your high school geometry course, you may
remember the theorem: The measure of an exterior angle of a triangle is
equal to the sum of the measures of its remote interior angles. That
result follows from a Euclidean parallel postulate; however, the following
theorem holds in any neutral geometry.
The next theorem will be useful in
proving two lines are parallel. From your high school geometry course, you may
remember the theorem: The measure of an exterior angle of a triangle is
equal to the sum of the measures of its remote interior angles. That
result follows from a Euclidean parallel postulate; however, the following
theorem holds in any neutral geometry.
Theorem 2.11. (Exterior Angle Theorem) Any exterior angle of a triangle is
greater in measure than either of its remote interior angles.
Outline of the proof. Let be given. Let D be a point such that A-C-D,
i.e.
is an exterior angle of
.
1. Let M be the midpoint of segment BC.
2. B-M-C and
3. There is a point E on ray AM such that A-M-E and ME = MA.
4.
5. and
are vertical angles.
6.
7.
8.
9.
10. E and D are on the same side of line BC.
11. B, M, E are on the same side of
line CD.
12.
13.
14.
15. The proof of the case for the other remote interior angle is similar.//
![]()
The Exterior Angle Theorem is used in the proof of the
Triangle
Inequality.
Theorem 2.12. Given a line and a point not on the line, there exists a unique
line perpendicular to the given line through the given point.
Theorem 2.13. Two lines perpendicular to the same line are parallel.
Theorem 2.14. There exist at least two lines that are parallel to each other.
![]() Theorem 2.15. If there is a transversal to two distinct lines with alternate
interior angles congruent, then the two lines are parallel.
Theorem 2.15. If there is a transversal to two distinct lines with alternate
interior angles congruent, then the two lines are parallel.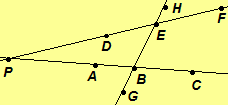
Outline of the proof. Assume line AB, line DE, and line BE are distinct with A-B-C, D-E-F, and G-B-E-H. Further, assume A
and D are on the same side of line BE. We will prove the contrapositive;
therefore, assume line AB and line DE are not parallel.
1. There exists a point P at the
intersection of line AB and line DE.
2. Without loss of generality, assume P
is on the same side of line BE as is A.
3. Consider
4. and
are exterior angles of
5. and
,
i.e.
and
6. and
//
 In general for a
neutral geometry,
the converse of the above theorem is not valid. The converse is valid in a
Euclidean geometry, which is discussed after the
Euclidean Parallel Postulate.
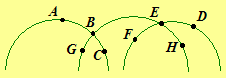
For an example where the converse is false, consider the Poincaré Half-plane and
the illustration on the left. Note that line AB is parallel to line DE, but
the alternate interior angles angle ABE and angle BEF are not
congruent. (Angle ABE is a right angle and angle BEF is an acute
angle.)
In general for a
neutral geometry,
the converse of the above theorem is not valid. The converse is valid in a
Euclidean geometry, which is discussed after the
Euclidean Parallel Postulate.
For an example where the converse is false, consider the Poincaré Half-plane and
the illustration on the left. Note that line AB is parallel to line DE, but
the alternate interior angles angle ABE and angle BEF are not
congruent. (Angle ABE is a right angle and angle BEF is an acute
angle.)
Exercise
2.55. For the Poincaré Half-plane, find all lines parallel to the given
line through the given point.
(a)
(2, 1) and (Note the notation error in the graphic
equation, it should read 1l
= {(x, y)... . The subscript is before the letter.)
(b) (2, 1) and
Exercise
2.56. Justify each step and fill in any gaps in the proof of the Exterior
Angle Theorem.
Exercise
2.57. Prove Theorem 2.12. (Hint. Use SAS Postulate to prove the
existence of a perpendicular line and Exterior Angle Theorem to prove
uniqueness.)
Exercise
2.58. Prove Theorem 2.13.
Exercise
2.59. (a) Prove that given a line and a
point not on the line, there is a line parallel to the given line and passing
through the point
not on the line.
(b)
Prove Theorem 2.14.
Exercise
2.60. Justify each step and fill in any gaps in the proof of the Theorem
2.15.
Exercise
2.61. State and prove the AAS Theorem for congruent triangles.