2.6.2 Saccheri Quadrilaterals![]()
![]() Printout
Printout
The value of non-Euclidean geometry lies in its ability to
liberate us from preconceived ideas in preparation for the time when
exploration of physical laws might demand some geometry other than the
Euclidean.
—![]() Georg Friedrich Bernhard Riemann (1826–1866)
Georg Friedrich Bernhard Riemann (1826–1866)
![]()
![]() Girolamo Saccheri (1667–1733), an
Italian Jesuit priest and mathematician, attempted to prove
Girolamo Saccheri (1667–1733), an
Italian Jesuit priest and mathematician, attempted to prove ![]() Eugenio
Beltrami (1835–1900).
Eugenio
Beltrami (1835–1900).
Saccheri considered a
certain type of quadrilateral, called a Saccheri
quadrilateral, as a basis for the beginning of his work in attempting to demonstrate
the Fifth Postulate. We consider Saccheri quadrilaterals here to show just how
close to the Euclidean concept of parallel lines one can arrive without
assuming the Fifth Postulate. Since the existence of a rectangle is equivalent
to
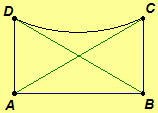
Definition.
A Saccheri
quadrilateral is a quadrilateral ABCD
where and
are right angles and
.
Segment
is called the base, and segment
is called the summit.
A parallelogram is a quadrilateral in which
both pairs of opposite sides are
parallel.
A rectangle is a
quadrilateral with four right angles.
 Theorem
2.16. The diagonals of a Saccheri quadrilateral are congruent.
Theorem
2.16. The diagonals of a Saccheri quadrilateral are congruent.
Theorem 2.17. The summit angles of a Saccheri quadrilateral are congruent.
Proof. Given Saccheri
quadrilateral ABCD with right angles and
,
and
By Theorem 2.16,
.
Since
,
,
and
,
we have
Hence
.
Therefore, the summit angles of a Saccheri quadrilateral are congruent.//
Theorem 2.18. The segment joining the midpoints of the base and summit of a
Saccheri quadrilateral is perpendicular to both the base and summit.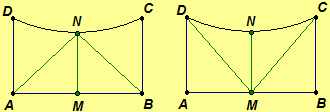
Proof. Given Saccheri
quadrilateral ABCD with right angles and
,
and
Further, assume M and N are the
midpoints
of segment AB and segment CD, respectively. Thus A-M-B, C-N-D,
,
and
Since the summit angles are congruent,
Since
,
,
and
,
we have
Hence
Since
,
,
and
,
we have
Hence
Since A-M-B,
and
are a
linear pair. Since a linear pair of
congruent angles are right angles,
and
are right angles. Hence, by the
definition of
perpendicular lines, line AB is
perpendicular to line MN. A similar
procedure may be used to prove line CD
is perpendicular to line MN.
Therefore, segment MN is
perpendicular to both segment AB and
segment CD.//
Theorem 2.19. The summit and base of a Saccheri quadrilateral are parallel.
Theorem 2.20. A Saccheri quadrilateral is a parallelogram.
It can be proven that the existence
of a rectangle is equivalent to 2.20,
the properties that a Saccheri quadrilateral and a rectangle have in common.
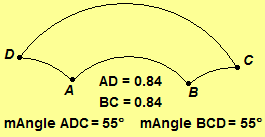
But, the Saccheri quadrilateral is not a rectangle without a Euclidean parallel
postulate. For an example of a Saccheri quadrilateral that is not a rectangle,
consider the Saccheri quadrilateral in the Poincaré Half-plane on the right.
The summit angles at C and D are not right angles, since their
value is less than 90. The Poincaré Half-plane is a model of a hyperbolic
geometry in which it can be shown that the summit angles of a Saccheri
quadrilateral measure less than 90.
Exercise
2.62.
Prove Theorem 2.16.
Exercise
2.63. Prove Theorem 2.19.
Exercise
2.64. Prove Theorem 2.20.