Perspective Dfns

4.6.1 Definitions for Perspectivity and Projectivity Printout
Mighty is geometry; joined with art, resistless.
—Euripides (480–406 B.C.)

A one-to-one mapping between a pencil of points and a pencil of lines is called an elementary correspondence if each point of the pencil of points is incident with the corresponding line of the pencil of lines. The elementary correspondence is denoted
or
. [An elementary correspondence is also called a perspectivity between a pencil of points and a pencil of lines.]
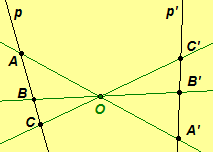
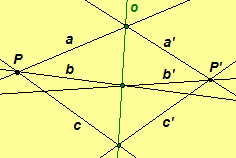
A one-to-one mapping between two pencils of points is called a perspectivity if the lines incident with the corresponding points of the two pencils are concurrent. The point where the lines intersect is called the center of the perspectivity. The perspectivity is denoted
where O is the center of perspectivity.
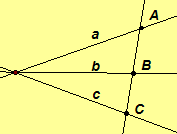
A one-to-one mapping between two pencils of lines is called a perspectivity if the points of intersection of the corresponding lines of the two pencils are collinear. The line containing the points of intersection is called the axis of the perspectivity. The perspectivity is denoted
where o is the axis of perspectivity.

Note that a perspectivity is a composition of two elementary correspondences between either two pencils of points or two pencils of lines.
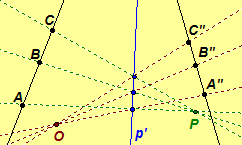
Illustrations of perspectivities: , , and an elementary correspondence .

Perspectivity between two pencils of points. Click for a javasketchpad illustration.

Perspectivity between two pencils of lines. Click for a javasketchpad illustration.

Elementary correspondence or perspectivity between a pencil of points and a pencil of lines. Click for a javasketchpad illustration.

Click here for a dynamic illustrations of perspectivity GeoGebra or JavaSketchpad.

A one-to-one mapping between two pencils of points is called a projectivity if the mapping is a composition of finitely many elementary correspondences or perspectivities. A projectivity is denoted
or
or
.

When a projectivity exists between two pencils, the pencils are said to be projectively related. Also, note that elementary correspondences and perspectivities themselves are projectivities.
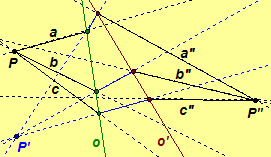
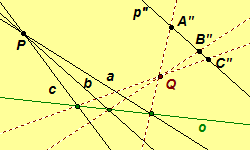
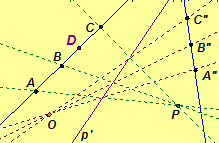
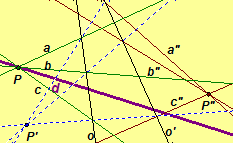
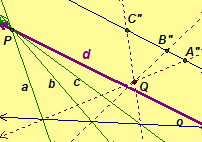
Illustrations of projectivities: Figure 1 , Figure 2 , and Figure 3 .

Projectivity between two pencils of points. Click for a javasketchpad illustration.

Projectivity between two pencils of lines. Click for a javasketchpad illustration.

Projectivity between a pencil of lines and a pencil of points. Click for a javasketchpad illustration.

Click here to explore dynamic illustrations of projectivity GeoGebra or JavaSketchpad.

To better see the projectivities in each figure, we describe a path to follow beginning with one of the points/lines and following the "path of its projection."

In Figure 1, from A follow the path with center P to axis p', from axis p' follow the corresponding path with center O to A".
In Figure 2, follow the path a from center P to axis o, from axis o follow the corresponding path from center P' to axis o' which leads to the corresponding path a" with center P".
In Figure 3, follow the path a from center P to axis o , then from axis o follow the corresponding path through center Q to A".

Exercise 4.28. Symbolize each perspectivity forming the projectivity in each of the above diagrams.

Exercise 4.29. Find the image of the point D or line d for each projectivity.

Find the image of D in the projectivity between two pencils of points.

Find the image of line d in the projectivity between two pencils of lines.

Find the image of line d in the projectivity between a pencil of lines and a pencil of points.

4.2.1 Axioms 4.3 Duality

4.5.2 Harmonics and Music4.6.2 Fundamental Theorem of Projective Geometry