4.5.2 Harmonic Sets and Music  Printout
There is geometry in the humming of the strings.
—Pythagoras (540 B.C.)

        The example and exercises on this page illustrate why the term harmonic sets is reasonable. The major diatonic scale (Just Diatonic Scale or scale of Zarlino - Gioseffo Zarlino, 1517–1594) consists of notes with the frequency ratios 1, 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, 2 relative to a key note. Though there are many different definitions and formulations of what chords are harmonic, the chords in the frequency ratios 1:2:3, 2:3:4, 3:4:5, and 4:5:6 are called harmonic.
        Consider the major triad with frequency ratio 4:5:6, which is equivalent to the ratio 1:5/4:3/2. With a string tuned to C, the frequency ratios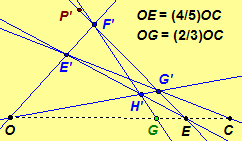 give the notes 1 (C), 9/8 (D), 5/4 (E), 4/3 (F), 3/2 (G), 5/3 (A), 15/8 (B), 2 (C). Hence, the ratio 4:5:6 (1:5/4:3/2) give the notes C, E, and G. Since the period is the reciprocal of the frequency, the ratio of the lengths of the string to the corresponding notes would be 1:4/5:2/3 for C, E, and G. We consider a string tuned to C with E 4/5 and G 2/3 of the length of the string. The following diagram illustrates that the points O, G, E, C form a harmonic set H(OE,CG); that is, G is the harmonic conjugate of C with respect to O and E.

Click here for a dynamic investigation of this relationship GeoGebra or JavaSketchpad.

You may use dynamic geometry software for each of the following exercises.

Exercise 4.25.  The frequency ratio 3:4:5 is equivalent to the ratio 1:4/3:5/3, which gives the chord F, A, C called the subdominant of the major triad of the example above. As with the example, show H(OF, CA) where OF is 3/4 of the length of OC and OA is 3/5 of the length of OC.

Exercise 4.26.  The frequency ratio 3:4:5 is also equivalent to the ratio 3/2:15/8:9/8, which gives the chord G, B, D called the dominant of the major triad of the example above. As with the example, show H(OG, DB) where OG = (2/3)OC,  OB = (8/15)OC, and OD = (8/9)OC.

Exercise 4.27.  A different scale called the equal temperament scale is used in tuning pianos. The frequency ratios are 1.000 (C) : 1.122 (D) : 1.260 (E) : 1.335 (F) : 1.498 (G) : 1.682 (A) : 1.888 (B).  If a string is tuned to C (as with the example above) and the equal temperament scale is used, investigate whether or not the major triad C, E, and G determines a harmonic set H(OE, CG).