4.5.1 Harmonic Sets  Printout
Music is the pleasure the human mind experiences from counting without being aware that it is counting.
—Gottfried Wilhelm von Leibniz (1646–1716)

       Desargues' Theorem and its dual gave a relationship between the vertices and sides of perspective triangles. We next consider relationships between certain points determined from a complete quadrangle. Consider a complete quadrangle EFGH. By Axiom 4, we know the diagonal points are never collinear. 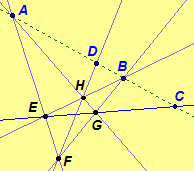But what are the properties of the four points, formed by a line through two diagonal points A and B, and by the line's (line AB) intersection with the remaining two sides of the complete quadrangle forming points C and D? Click here for a javasketchpad illustration GeoGebra or JavaSketchpad.
        These points are called a harmonic set. A motivation for this name will come in several exercises where we will relate harmonic sets to musical scales.

Definition. Four collinear points are said to be a harmonic set if there exists a complete quadrangle such that two of the points are diagonal points of the complete quadrangle and the other two points are on the opposite sides determined by the third diagonal point.

Notation. Four collinear points A, B, C, D form a harmonic set, denoted H(AB, CD), if A and B are diagonal points of a complete quadrangle and C and D are on the sides determined by the third diagonal point. The point C is the harmonic conjugate of D with respect to A and B. Also, D is the harmonic conjugate of C with respect to A and B.

        Note in the example of the above diagram, we have the harmonic set H(AB, CD). The four collinear points  A, B, C, and D are such that A = EF · GH and B = EH · FG are diagonal points of a complete quadrangle EFGH, and C is on EG and D is on FH where EG · FH is the third diagonal point of the complete quadrangle EFGH.
        Further, note that H(AB, CD), H(BA, CD), H(AB, DC), and H(BA, DC) all represent the same harmonic set of points. The points that are diagonal points of the complete quadrangle are listed first and the two conjugate points are listed second.

        Several natural questions arise about harmonic sets. Does a harmonic set of points exist? Given three collinear points, can a harmonic set of points be constructed? If the answer is yes, is the harmonic set unique or does it depend on the complete quadrangle defining the points? How can we determine when a set of four collinear points is a harmonic set? Do H(AB, CD) and H(CD, AB) both exist? If so, are they related to each other?

        We begin by investigating the first question. In an exercise in the section on basic theorems, we proved the existence of a complete quadrangle. From this result, it follows that a harmonic set of points must exist. One of the exercises assigned at the end of this section is to write the proof.

         Now consider the second question. Let A, B, and C be three distinct collinear 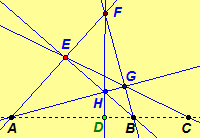points. There is a point E such that the three points A, C, and E are noncollinear. (Why?) Let F be a point on line AE distinct from A and E. (How do we know F exists?) Let G = CE · BF and H = AG · BE. We assert that E, F, G, and H determine a complete quadrangle. We need to show that the points are distinct and no three are collinear. If G = F, then A, E, G = F, and C would be collinear since A is on EF and G = F is on CE. But this is a contradiction since A, C, and E are noncollinear. Hence, G and F are distinct points. Arguments can be made for the other cases showing that E, F, G, and H are distinct points. (Check them.) Suppose E, F, and G are collinear. Since G, F, and C are on lines BF, AE, and AB, respectively, we have that points A, C, and E are collinear, a contradiction. Hence E, F, and G are noncollinear. An argument can be made for the other cases. (Check them.) Hence, EFGH is a complete quadrangle with A = EF · GH, B = EH · FG, and C = EG · AB. Thus, since FH is the remaining side of the complete quadrangle EFGH, we define D = FH · AB. Therefore, A, B, C, and D are four points in a harmonic set of points.

Exercise 4.20.  Prove that D is distinct from A, B, and C.

        By the above results, we have actually proven the following two theorems. (The first video is the lecture and this second video is the construction in Geometer's Sketchpad.)

Theorem 4.5. There exists a harmonic set of points.

Theorem 4.6. If A, B, and C are three distinct collinear points, then a harmonic conjugate of C with respect to A and B exists.

        The proof for Theorem 4.6 was constructive. Hence, by following the steps of the proof, we can determine a fourth point to form a harmonic set by construction. Given three collinear points A, B, and C, construct a harmonic conjugate of C with respect to A and B by the following steps. (Click here for a dynamic illustration of the steps GeoGebra or JavaSketchpad.)

• Let E be a point not on line AB and F be a point on line AE.
• Let G = CE · BF and H = AG · BE.
• Let D = FH · AB.

Hint for exercises involving the dual: Translate the above steps to give a procedure for the construction of a harmonic set of lines.

Justification for the term harmonic set could now be presented. See the examples in Harmonics and Music.

We now consider the next question in our list. Is the fourth point unique or does it depend on the complete quadrangle constructed?

• What happens when E and F are moved?
• Does the complete quadrangle remain the same?
• Does the fourth point, D, of the harmonic set remain in the same position?

Click here to investigate this question with a dynamic diagram  GeoGebra or JavaSketchpad..

        Based on this investigation, we conjecture the following theorem, which implies that the fourth point in the construction is independent of the choice of point E and F. That is, the fourth point does not depend on the complete quadrangle, it only depends on the initial three points A, B, and C.

Theorem 4.7. If A, B, and C are three distinct collinear points, then the harmonic conjugate of C with respect to A and B is unique.

Proof.  (We will use Desargues' Theorem and its dual.) Let A, B, and C be three distinct collinear points. By Theorem 4.6, D a harmonic conjugate of C with respect to A and B exists. 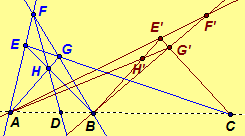Let EFGH be a complete quadrangle used to construct D with A = EF · GH, B = EH · FG, C = EG · AB, and D = FH · AB. Let D'  also be a harmonic conjugate of C with respect to A and B that is constructed from a different complete quadrangle E'F'G'H' with A = E'F' · G'H', B = E'H' · F'G', C = E'G' · AB, and D' = F'H' · AB. We assert that D = D'.
        By the definition of two triangles perspective from a line, triangle EFG and triangle E'F'G' are perspective from line AB. Thus, by the dual of Desargues' Theorem, the triangle EFG and triangle E'F'G' are perspective from a point. Hence,the lines EE', FF', and GG' are concurrent. Similarly,  from triangles EGH and E'G'H',  the lines EE', GG', and HH' are concurrent. Since the lines EE', FF', GG', and HH' are all concurrent, triangle FGH and triangle F'G'H' are perspective from a point. Hence, by Desargues' Theorem, triangle FGH and triangle F'G'H' are perspective from a line. Therefore, GH · G'H' = A, FG · F'G' = B, and FH · F'H' are collinear. That is, FH · F'H' is on line AB. Hence D = FH · AB = F'H' · AB = D'.
        Therefore, the harmonic conjugate of C with respect to A and B is unique.//

        Now we consider the last of our questions. Do H(AB, CD), and H(CD, AB) both exist? If so, are they related to each other? Since the above theorems state that we can find a unique fourth point given three collinear points, we would probably guess that the two harmonic sets are the same. That is, if we began with C, D, and A, we would expect to obtain B with our construction. Then B is the harmonic conjugate of A with respect to C and D.

Theorem 4.8. H(AB, CD) if and only if H(CD, AB).

Proof. We show one direction of the biconditional, the proof of the converse is similar. Since H(AB, CD), 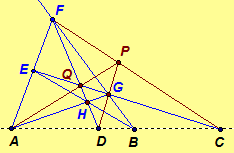there is a complete quadrangle EFGH such that A = EF · GH, B = EH · FG, C = EG · AB, and D = FH · AB. We desire a complete quadrangle with C and D as diagonal points and A and B determined from the remaining pair of opposite sides.
        Let P = CF · DG and Q = FH · EG. Note that each set {F,P,C}, {F,G,B}, {F,Q,H,D}, {E,Q,G,C}, and {P,G,D} is a collinear set. Further, no three of  F, G, P, Q are collinear. Now consider complete quadrangle FGPQ, then PF · GQ = CF× EG = C, FQ× PG = FH× DG = D, and FG× DC = B. We only need to show that PQ · DC = A.
        Triangle EHQ and triangle FGP are perspective from a line, since B = EH · FG, C = EQ · FP, and D = HQ · GP are collinear. Hence by the dual of Desargues' Theorem, they are perspective from a point. Thus, since EF · HG = A, PQ contains A, which implies that PQ · DC = A.
        Therefore, if H(AB, CD), then H(CD, AB). The proof of the converse is similar.//

        Thus using the definition of a harmonic set of points and Theorem 4.4, the following corollary is obtained.

Corollary 4.9. The following are equivalent: H(AB, CD), H(AB, DC), H(BA, CD), H(BA, DC), H(CD, AB), H(CD, BA), H(DC, AB), and H(DC, BA).

Exercise 4.21.  Consider the dual of a harmonic set of points.

1. Write the definition for the dual of a harmonic set of points.
2. Write the dual for each of the four theorems.
3. Prove the theorems stated in part (b). (Hint. Use the principle of duality.)

Exercise 4.22. Write the proof for Theorem 4.5, the existence of a harmonic set of points that was briefly described in this section.

Exercise 4.23. Construct each of the following where the points or lines are located as in each illustration. (You may use dynamic geometry software.)

1. Construct the harmonic conjugate of C with respect to A and B. 
2. Construct the harmonic conjugate of C with respect to A and B. 
3. Construct the harmonic conjugate of c with respect to a and b. 
4. Construct the harmonic conjugate of c with respect to a and b.  

Exercise 4.24. Let M be the midpoint of a Euclidean segment AB. Determine, if possible, the harmonic conjugate of M with respect to A and B.  (Hint. Use dynamic geometry software to help investigate.)

Music creates order out of chaos: for rhythm imposes unanimity upon the divergent, melody imposes continuity upon the disjointed, and harmony imposes compatibility upon the incongruous.
—Yehudi Menuhin (1916–1999)