Solution Exercise 4.21.
Definition of Term Commonly Used in Mathematics:
By a Previous Theorem – I do not remember how it goes, but if I stated it right, then the rest of this follows.

Exercise 4.21.  Consider the dual of a harmonic set of points.
(a)  Write the definition for the dual of a harmonic set of points.

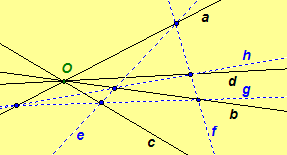Four concurrent lines are said to be a harmonic set of lines if there exists a complete quadrilateral such that two of the lines are diagonal lines of the quadrilateral and the other two lines contain the opposite vertices determined by the third diagonal line.

Notation. Four concurrent lines a, b, c, d form a harmonic set, denoted H(ab, cd), if a and b are diagonal lines of a quadrilateral and c and d contain the points determined by the third diagonal line. The point c is the harmonic conjugate of d with respect to a and b. Also, d is the harmonic conjugate of c with respect to a and b.

(b)  Write the dual for each of the four theorems.

Dual of Theorem 4.5. There exists a harmonic set of lines.
Dual of Theorem 4.6. If a, b, and c are three distinct concurrent lines, then a harmonic conjugate of c with respect to a and b exists.
Dual of Theorem 4.7. If a, b, and c are three distinct concurrent lines, then the harmonic conjugate of c with respect to a and b is unique.
Dual of Theorem 4.8. H(ab, cd) if and only if H(cd, ab).

(c)  Prove the theorems stated in part (b).

The results follow immediately from the corresponding theorems since the projective geometry satisfies the principal of duality.