4.3 Duality in Projective Geometry  Printout
I think and think for months and years, ninety-nine times, the conclusion is false. The hundredth time I am right.
—Albert Einstein (1879–1955)

Remember that the dual of a statement was defined in the section on axiomatic systems in the first chapter.

In this section, we show that plane projective geometry satisfies the principle of duality. Remember that once we have proven a theorem, by the principal of duality, the dual of the theorem is also valid, i.e., one proof proves two statements.

Note that the first two axioms are nearly the duals of each other.
        Axiom 1. Any two distinct points are incident with exactly one line.
        Axiom 2. Any two distinct lines are incident with at least one point.
In the last section on basic theorems, the dual of Axiom 1 was stated and you worked out its proof.

Dual of Axiom 1. Any two distinct lines are incident with exactly one point.

Exercise 4.11. For Axiom 2, write the dual and its proof..

Note that neither of the first two axioms or their duals provide for the existence of any points or lines. However, Axiom 3 and its dual state that at least four points and four lines exist.

Dual of Axiom 3. There exist at least four lines, no three of which are concurrent.

Proof. Let A, B, C, and D be four distinct points, no three collinear; the existence of these points is given by Axiom 3. Thus by Axiom 1, and since no three of the points are collinear, there are six distinct lines AB, AC, AD, BC, BD, and CD.
        Consider the four lines AB, BC, CD, and DA. We assert that no three of these lines are concurrent. Suppose not, then three of the lines would be concurrent, say AB, BC, and CD are concurrent. By the Dual of Axiom 1, B  is the only point of intersection of AB and BC. Hence B is the point of concurrency for the three lines AB, BC, and CD. Thus B is on CD, which contradicts the initial assumption that B, C, and D are noncollinear. The other cases follow from a similar argument.
        Therefore, there exist at least four lines, no three of which are concurrent.  //

Before examining the Dual of Axiom 4, we need to define a complete quadrilateral, which is the dual of a complete quadrangle. Also, note some of the differences between complete quadrangles and complete quadrilaterals as well as differences between complete quadrilaterals and Euclidean quadrilaterals.

Definition. A complete quadrilateral is a set of four lines, no three of which are concurrent, and the six points incident with each pair of these lines. The four lines are called sides and the six points are called vertices of the quadrilateral. Two vertices of a complete quadrilateral are opposite if the line incident to both points is not a side. A diagonal line of a complete quadrilateral is a line incident with opposite vertices of the quadrilateral.

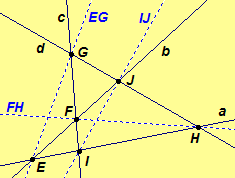Model. The sides of the quadrilateral abcd are a, b, c and d. The vertices of the quadrilateral are E = a · b, F = b · c, G = c · d, H = a · d, I = a · c and J = b · d. The opposite vertices are E & G, F & H, and I & J. The diagonal lines of the quadrilateral are EG, FH, and IJ. Click here to investigate a quadrilateral GeoGebra or JavaSketchpad.

Note that unlike a triangle, which is similar in definition to a Euclidean triangle, the quadrangle and quadrilateral do not have similar analogues in Euclidean geometry. Also, unlike in Euclidean geometry, the quadrangle and quadrilateral are different figures.

Dual of Axiom 4. The three diagonal lines of a complete quadrilateral are never concurrent.

Proof. Let abcd be a complete quadrilateral; the existence is given by the Dual of Axiom 3. Let E = a · b, F = b · c, G = c · d, H = a · d, I = a · c and J = b · d, these points exist and are unique by the Dual of Axiom 1. By Axiom 1 and the definition of diagonal lines, the diagonal lines EG, FH, and IJ exist.
        We assert that the diagonal lines are not concurrent. Suppose the diagonal lines EG, FH, and IJ are concurrent. Since EG · FH would be the point of concurrency, the points I, J, and EG · FH are collinear . Since abcd is a complete quadrilateral, no three of the lines a = EH, b = EF, c = FG, and d = GH are concurrent. Thus, (by a proof that is the dual of the proof for the Dual of Axiom 3) E, F, G, and H are four points, no three of which are collinear. Hence, EFGH is a complete quadrangle with diagonal points EF · GH = b · d = J, EG · FH, and EH · FG = a · c = I. Thus, by Axiom 4, the points I, J, and EG · FH are noncollinear, which contradicts that they are collinear. Therefore, the diagonal lines of the complete quadrilateral abcd are not concurrent. //

Click here for a dynamic illustration of Desargues' Theorem with either GeoGebra or JavaSketchpad.

Dual of Axiom 5. (Dual of Desargues' Theorem) If two triangles are perspective from a line, then they are perspective from a point.

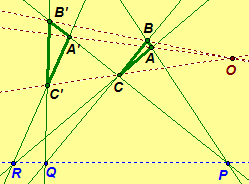Proof. Assume triangle ABC and triangle A'B'C' are perspective from a line with P = AB · A'B', Q = BC · B'C' and R = AC · A'C'. By the definition of perspective from a line, the points P, Q and R are collinear. Let O = AA' · BB'. To show that AA', BB' and CC' are concurrent, we only need to show that O is on the line CC'.
     Consider triangles RAA' and QBB'. Since P, Q, R are collinear, P is on line QR. Since P = AB · A'B', P is on line AB and line A'B'. Hence triangles RAA' and QBB' are perspective from point P, by the definition of perspective from a point. Thus by Axiom 5 (Desargues' Theorem), triangles RAA' and QBB' are perspective from a line. By the definition of perspective from a line, the points C = RA · QB, C' = RA' · QB' and O = AA' · BB' are collinear. Hence O is on line CC'. Thus AA', BB' and CC' are concurrent. Therefore, triangle ABC and triangle A'B'C' are perspective from point O.  //
 

Definitions for perspectivity and projectivity for pencils of points and lines.

Dual of Axiom 6. If a projectivity on a pencil of lines leaves three distinct lines of the pencil invariant, it leaves every line of the pencil invariant.

Exercise 4.12.
        (a) How many cases are there in the proof of the Dual of Axiom 3?
        (b) State the other cases.
        (c) Prove at least one of the cases.

Exercise 4.13.
        (a) Prove the existence of a complete quadrilateral.
        (b) What are similarities and differences between complete quadrilaterals and complete quadrangles.
        (c) What are similarities and differences between complete quadrilaterals and Euclidean quadrilaterals.

Exercise 4.14.
        (a)  Prove that every point is incident with at least three distinct lines.
        (b)  Prove that every point is incident with at least four distinct lines.

Exercise 4.15. Prove the Dual of Axiom 6.