TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

Triangle Inequality  Printout
Proof is the idol before whom the pure mathematician tortures himself.
—Sir Arthur Eddington (1882–1944)

      On this page, we prove the Triangle Inequality based on neutral geometry results from Chapter 2.

Lemma. In a neutral geometry, if one angle is greater in measure than another angle of a triangle, then the opposite side of the greater angle is longer than the opposite side of the lessor angle. Furthermore, the longest side of a triangle is opposite the angle of greatest measure.

  Proof.  Given . Assume  Let A' 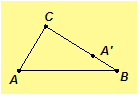be on ray  such that  Then  One of the following three is true: B is between C and A'; A' = B; or A' is between C and B.

      Case 1. Assume B is between C and A'. Then  and by the Exterior Angle Theorem  Thus  Hence , which contradicts the initial assumption. Hence B is not between C and A'.
      Case 2. Assume A' = B. Then  Hence , which contradicts the initial assumption.
      By Cases 1 and 2, we must have A' between C and B. Hence, BC = BA' + A'C > A'C = AC. The cases for the other pairs of sides may be proved similarly. Therefore, the longest side of a triangle is opposite the angle of greatest measure.//

Triangle Inequality. In a neutral geometry, the length of one side of a triangle is strictly less than the sum of the lengths of the other two sides.

Proof.  Given . We prove 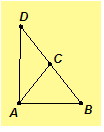one case here; the other cases are similar. Let D be on ray  such that C is between B and D and  Since  is an isosceles triangle,  Since C is between B and D and , , by the Angle Addition Postulate. Hence  By the Lemma, BD > BA. Therefore, since C is between B and D, AC + CB = DC + CB = DB > BA. Since the proofs of the other two cases are similar, the length of one side of a triangle is strictly less than the sum of the lengths of the other two sides.//