TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

            3.4.2 Translations and Rotations for the Analytic Euclidean Plane Model Printout
In a few minutes, a computer can make a mistake so great that it would take many men many months to equal it.
 —Merle L. Meacham

 

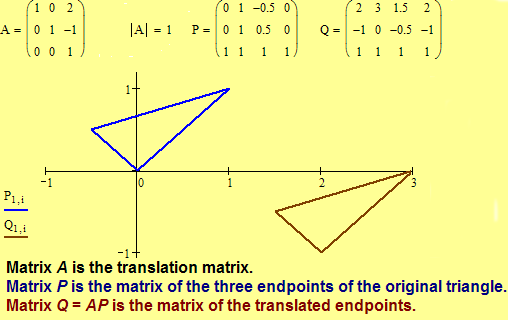
      The investigations from the last section indicate that a translation or a rotation of the Euclidean plane is a direct isometry. What form does the matrix of an affine translation of the Euclidean plane have? Let's investigate that question. Let T_PQ be an affine translation of the Euclidean plane with vector PQ = (a, b, 0) and let A be the translation matrix.  Let X(x₁, x₂, 1) be an arbitrary point in the Euclidean plane with image X' under the translation T_PQ.

 

Since XX' = PQ,  for every X in the plane. Hence,  and  for every X in the plane. Since the two expressions are true for all points X, we substitute with particular values for the point X. Let X = (0, 0, 1), then a₁₃ = a and a₂₃ = b. Let X = (1, 0, 1), then a₁₁ – 1 + a = a and a₂₁ + b = b. Hence, a₁₁ = 1 and a₂₁ = 0.  Finally, let X = (0, 1, 1), then a₁₂ + a = a and a₂₂ – 1 + b = b. Hence, a₁₂ = 0 and a₂₂ = 1. Hence,

 

Since the det(A) = 1, a translation is a direct isometry. We summarize our results above and from the previous section with the following proposition.  (Part (b) is left for you to verify in Exercise 3.65.)

 

Proposition 3.13. (a) An affine translation of the Euclidean plane is a direct isometry. (b) Any affine direct isometry of the Euclidean plane with no invariant points is a translation. (c) The matrix representation of an affine translation of the Euclidean plane T_PQ, defined by vector PQ = (a, b, 0), is

 

Click here to view an animation of the following example.

 

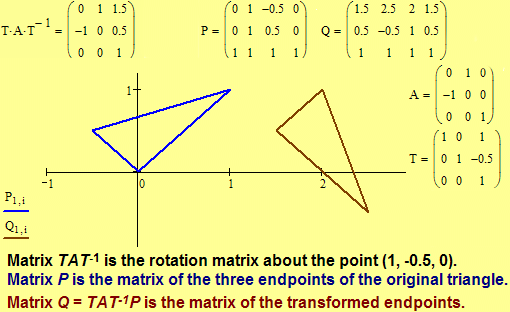
      Next, we investigate the form of the matrix of an affine rotation of the Euclidean plane. To simplify the problem, we first consider the problem with the center of rotation at the origin. Let  be an affine rotation of the Euclidean plane with center O(0, 0, 1) and let A be the translation matrix. We proceed in a similar manner as with the derivation for the translation matrix. Let X(x₁, x₂, 1) be an arbitrary point in the Euclidean plane with image X' under the rotation .

  

Since the center of a rotation is invariant, O(0, 0, 1) maps to itself; therefore, the matrix must be of the form

 

By trigonometric definitions of the circular functions,  maps the point (1, 0, 1) to  and the point (0, 1, 1) to . Hence,    and  Hence, A has the form

 

Note that the det(A) = 1, hence, A is the matrix of a direct isometry. We must show that A is the matrix of the rotation. Since A is the matrix of an isometry, XO = X'O for any point X distinct from the center O. Once we show that for any point X distinct from O, , by definition matrix A would be the matrix of the rotation . Since X' = AX, we have  The sides of  are contained in the lines  and  Substitute into the formula for the angle between two lines,

 

      If the center of rotation, C, is at a point other than the origin O, we translate the center C to the origin, rotate about the origin, and translate back to C, i.e.  We summarize our results above and from the previous section with the following proposition. (Part (b) and (d) are left for you to verify in Exercise 3.65.)

 

Proposition 3.14. (a) An affine rotation of the Euclidean plane is a direct isometry. (b) Any affine direct isometry of the Euclidean plane with one invariant point is a rotation. (c) The matrix representation of an affine rotation of the Euclidean plane with center O(0, 0, 1) is

 

(d) The matrix representation of an affine rotation of the Euclidean plane with center C not at O is  

Click here to view an animation of the following example.

 

Exercise 3.57. Find a matrix of the translation that maps the point X(3, 8, 1) to Y(5, 1, 1) and find the image of Z(12, 7, 1). Is the matrix unique?

Exercise 3.58. Find a matrix of the translation that maps the line l[2, 3, –1] to m[2, 3, 5]. Is the matrix unique? 

Exercise 3.59. Find a matrix of the rotation   where C(2, 1, 1) and find the image of X(3, 6, 1).
Exercise 3.60. Find a direct isometry that maps X(1, 1, 1) to X'(–1, 1, 1) and Y(3, 0, 1) to Y'(0, 3, 1). Is it a translation or a rotation?

 

Exercise 3.61. Let the point of intersection of the lines l[1, –1, 0] and m[1, 1, –2] be the center of a rotation that maps l to m. Find the matrix of a rotation that maps l to m.

Exercise 3.62. Let the point of intersection of the lines l[–1, 5, 1] and m[3, –2, 4] be the center of a rotation that maps l to m. Find the matrix of a rotation that maps l to m.

 

Exercise 3.63. What is the form of the inverse of an affine translation of the Euclidean plane? Affine rotation?

Exercise 3.64. Prove the set of affine translations of the Euclidean plane is a group under matrix multiplication.

 

Exercise 3.65. (a) Verify part (b) of Proposition 3.13.  (b) Verify part (b) of Proposition 3.14.  (c) Verify part (d) of Proposition 3.14.

Exercise 3.66. Prove the set of affine rotations of the Euclidean plane with center C is a group under matrix multiplication.

 

3.4.1 Translation and Rotation3.5.1 Reflection and Glide Reflection

© Copyright 2005, 2006 - Timothy Peil