Fractions, Number Lines, and Order

Ordering Fractions

We use a number line model to illustrate fraction order for values between 0 and 1. We divide that length into two equal-sized pieces and label the point where the segment is divided with the coordinate 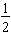. The distance from 0 to 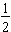 represents a length of one-half the whole segment from 0 to 1.

We further divide each of those halves in half; the points where each segment is divided are represented by the fractions  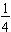and 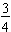.   As with equivalent fractions from the previous session, we may label the point at 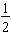   as 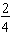, that is, this is another way to visualize equivalent fractions.

The next diagrams illustrate an extension of fraction order relationships to twelfths, sixths, fourths, thirds, and halves, and how they relate to each other on the segment between 0 and 1.

We bring these number lines together in the illustration below to a single number line with the coordinates labeled with the simplified form for each of the fractions in the above illustration.

When we compare values, the one that is farthest to the left on the number line has the least value. Looking at the diagram below, we see that  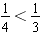(circled values).  Likewise, we see that 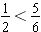 (boxed values).

If we did not refer to a completed number line, we could still determine these inequalities by changing each pair of fractions to fractions with common denominators.

Examples:  

Since 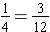, , 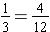and 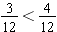, we have 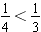. Twelfths is a common denominator for fourths and thirds.

Since  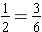and 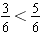, we have 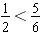. Sixths is a common denominator for halves and sixths.

 

Further note that we could have compared all four of the fractions 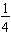, , 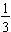, 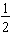and  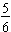by changing them all to the common denominator of twelfths. Since 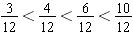, we have 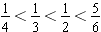. By converting the fractional values to fractions with common denominators, we are able to easily compare their relative sizes. 

 

Notice that the least common denominator is the least common multiple (LCM) of 2, 3, 4, and 6. The value of the LCM(2, 3, 4, 6) is 12 as illustrated below with the set intersection method for finding the least common multiple.

Reminder: we can also find the least common multiple (LCM) by prime factorization into the exponential form.

2 = 2 3 = 3 4 = 22 6 = 2 · 3

Taking the largest exponent of each prime factor we get   22 · 3 = 4 · 3 = 12.    So, LCM(2, 3, 4, 6) = 12.

 

return to top | previous page | next page