Solve and compare the following two problems.
Kim made one out of three free throws in a game and one out of four free throws in the next game. What fractional part of the free throws did Kim make?
Pat walked one-third of a mile in the morning and one-fourth of a mile in the evening. What fractional part of a mile did Pat walk?
We begin with these two examples to illustrate one of the reasons many people have problems with addition and subtraction of fractions.
Example from above: Kim made one out of three free throws in a game and one out of four free throws in the next game. What fractional part of the free throws did Kim make?
Kim made two-sevenths of the free throws, or Kim made two out of seven free throws.
Important Note. Here, we did a union of two disjoint sets as with addition of whole numbers. But we do not consider this to be the addition of two fractions since the size of the whole is different for each fraction. Each fraction is referencing a different sized whole object. We used the symbol 
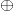to indicate that it is a different type of addition and not the addition of fractions. This also shows a common error in adding fractions that many people make, which is adding both the numerators and the denominators.
Example from above: Pat walked one-third of a mile in the morning and one-fourth of a mile in the evening. What fractional part of a mile did Pat walk?
Pat walked seven-twelfths of a mile.
Note. Each of the above problems is a type of addition. The first problem is not the addition of fractions, because the size of the whole is different for each fraction. But the second problem is an example of how we will define addition of fractions where the size of the whole is the same for each fraction.
Content ©2010. All Rights Reserved.
Date last modified: June 1, 2010.
Created with SoftChalk LessonBuilder
By Kris Montis and Timothy Peil
